Question 1.
Answer:
Let
⇒ x = A(x + 2) + B(x + 1)
⇒ x = (A + B)x + 2A + B
Comparing the coefficients of x and constant terms in both sides, we have
A + B = 1, 2A + B = 0
Now, solving these equations, we get
A = - 1 and B = 2
∴
∴ d x
= - log |x + 1| + 2 log |x + 2| + C
= - log |x + 1| + log |x + 2|2 + C
= log + C (∵ (x + 2)2 > 0)
Question 2.
Answer:
Let
=
⇒ 1 = A(x + 3) + B(x - 3)
⇒ 1 = A(A + B)x + 3A - 3B
Comparing the coefficients of x and constant terms in both sides, we have
A + B = 0 and 3A - 3B = 1
Now, solving these equations, we have

Question 3.
Answer:
Let
=
⇒ 3x - 1 = A(x - 2) (x - 3) + B(x - 1) (x - 3) + C(x - 1) (x - 2)
⇒ 3x - 1 = A(x2 - 5x + 6) + B(x2 - 4x + 3) + C(x2 - 3x + 2)
⇒ 3x - 1 = (A + B + C)x2 + (- 5A - 4B - 3C)x + 6A + 3B + 2C
Comparing the coeffcients of x2, x and constant terms in both sides, we have
A + B + C = 0
- 5A - 4B - 3C = 3
and 6A + 3B + 2C = - 1
Now, solving these equations, we get
A = 1, B = -5, C = 4
Alternative:
(3x - 1) = A(x - 2) (x - 3) + B(x - 1) (x - 3) + C(x - 1) (x - 2)
Putting x = 1
3 × 1 - 1 = A(1 - 2) (1 - 3)
⇒ 2 = A(- 1)(- 2)
⇒ 2 = 2A
⇒ A = 1
Putting x = 2
3 × 2 - 1 = B(2 - 1) (2 - 3) = B(- 1)
⇒ 6 - 1 = - B
∴ B = - 5
Putting x = 3
3 × 3 - 1 = C(3 - 1)(3 - 2)
⇒ 9 - 1 = C × 2 × 1
⇒ 8 = 2C
∴ C = 4
Values of A, B and C also obtain in this method.
Question 4.
Answer:
Let
⇒ x = A(x - 2) (x - 3) + B(x - 1) (x - 3) + C(x - 1) (x - 2) .... (1)
Putting x = 1 in equation (1), we get
1 = A(1 - 2) (1 - 3) + 0 + 0
⇒ 1 = A( - 1) (- 2) = 2A
∴ A =
Putting x = 2 in equation (1), we get
2 = B(2 - 1) (2 - 3)
⇒ 2 = B(1) (- 1)
⇒ 2 = - B
∴ B = - 2
Putting x = 3 in equation (1), we get
3 = C(3 - 1) (3 - 2) = C(2) × 1
⇒ 3 = 2C
C = 
Question 5.
Answer:
Let
⇒
⇒ 2x = A(x + 2) + B(x + 1)
Putting x = - 1 in equation (1), we get
2 × (- 1) = A(- 1 + 2)A
- 2 = A
∴ A = - 2
Putting x = - 2 in equation (1). we get
2 × (- 2) = B(- 2 + 1) = - B
⇒ - 4 = - B
∴ B = 4
∴
∴
= - 2 log |x + 1| + 4 log |x + 2| + C
= 4 log |x + 2| - 2 log |x + 1| + C
Question 7.
Answer:
Let
⇒ x = A(x2 + 1) + (Bx + C) (x - 1)
⇒ x = A(x2 + 1) + (Bx2 + Cx - Bx - C)
⇒ x = (A + B)x2 + (C - B)x + A - C
Comparing the coefficeint of x2, and constant terms in both sides, we have
A + B = 0, C - B = 1, A - C = 0
Now, solving these equation, we get

Alternative: ∫
Putting x2 + 1 = t
⇒ 2x dx = dt ⇒ x dx =
∴
= log |t| + C1
= log |x2 + 1| + C1
Question 8.
Answer:
Let
⇒ x = A(x - 1) (x - 2) + B(x + 2) + C(x - 1)2 ......... (1)
Putting x = 1 in equation (1), we get
1 = B(1 + 2) = 3B
∴ B =
Putting x = - 2 in equation (1), we get
- 2 = C(- 2 - 1)2
⇒ - 2 = C(- 3)2 = 9C
∴ C = -
Again, from equation (i), we have
x = A(x2 + x - 2) + B(x + 2) + c(x2 - 2x + 1)
⇒ x = (A + C)x2 + (A + B - 2C)x - 2A + 2B + C
Comparing the coefficients of x2, x and constant terms in both sides, we get
A + C = 0
A + B - 2C = 1
and - 2A + 2B + C = 0
On solving these equations, we get
Then A =

Question 9.
Answer:
⇒ 3x + 5 = A(x - 1) (x + 1) + B(x + 1) + C(x - 1)2
⇒ 3x + 5 = A(x2 - 1) + B(x + 1) + C(x2 - 2x + 1)
⇒ 3x + 5 = (A + C)x2 + (B - 2C)x - A + B + C
Comparing the coefficeints of x2, x and constant terms in both sides, we get
A + C = 0, B - 2C = 3, - A + B + C = 5
Now, solving these equations, we get
Question 10.
Answer: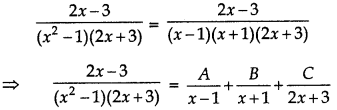
⇒ 2x - 3 = A(x + 1) (2x + 3) + B(x - 1) (2x + 3) + C(x - 1) (x + 1) ..... (1)
Putting x = 1 in equation (1), we get
2 × 1 - 3 = A(1 + 1) (2 × 1 + 3)
⇒ 2 - 3 = A × 2 × 5 = 1OA
⇒ - 1 = 10A
⇒ A = -
Putting x = - 1 in equation (1), we get
2 × (- 1) - 3 = B( - 1 - 1) (2 × (- 1) + 3)
⇒ - 2 - 3 = B(- 2) (- 2 + 3) = - 2B
⇒ 2B = 5 ⇒ B =
Putting x = - in equation (1), we get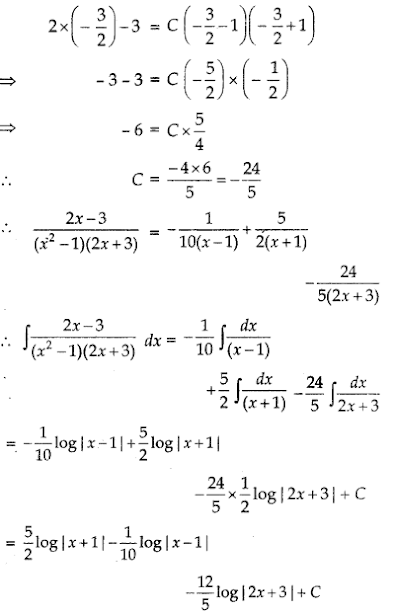
Question 11.
Answer: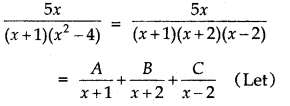
∴ 5x = A(x - 2) (x + 2) + B(x + 1) (x - 2) + C(x + 1) (x + 2) ...... (1)
Putting x = - 1 in equation (1), we get
5 × (- 1) = A(- 1 - 2) (- 1 + 2)
⇒ - 5 = A(- 3)(1) = - 3A
∴ A =
Putting x = -2 in equation (1), we get
5 × (- 2) = B(- 2 + 1) (- 2 - 2)
⇒ - 10 = B(- 1) (- 4) = 4B
∴ B = - = -
Putting x = 2 in equation (1), we get
5 × 2 = C(2 + 1) (2 + 2)
⇒ 10 = c(3) (4)
Question 12.
Answer:
Here, the given integrand is an improper rational function.
Divide x3 + x + 1 by x2 - 1, we get
⇒ 2x + 1 = A(x + 1) + B(x - 1)
Putting x = 1 in equation (1), we get
2 × 1 + 1 = A(1 + 1) + 0
⇒ 3 = 2A
∴ A =
Again putting x = - 1 in equation (1), we get
2(- 1) + 1 = B(- 1 - 1) = - 2B
⇒ - 2 + 1 = - 2B .
⇒ - 1 = - 2B
Question 13.
Answer:
⇒ 2 = A(1 + x) + (Bx + C) (1 - x)
⇒ 2 = A + Ax2 + Bx - Bx2 + C - Cx
⇒ 2 = (A - B)x2 + (B - C)x + A + C
Comparing the coefficients of x2, x and constant terms in both sides, we get
A - B = 0, B - C = 0, A + C = 2
Now, solving these equation, we get
A = 1, B = 1, C = 1
Question 14.
Answer:
⇒ 3x - 1 = A(x + 2) + B
⇒ 3x - 1 = Ax + 2A + B
Comparing the coefficient of x and constant terms in both sides, we get
A = 3, 2A + B = - 1
⇒ 2 × 3 + B = - 1
∴ B = - 1 - 6 = - 7
Question 15.
Answer: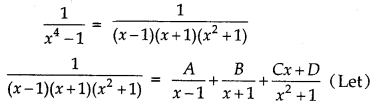
⇒ 1 = A(x + 1) (x2 + 1) + B(x2 + 1) (x - 1) + (Cx + D) (x - 1) (x + 1)
⇒ 1 = A(x3 + x2 + x + 1) + B(x3 - x2 + x - 1) + (Cx + D) (x2 - 1)
⇒ 1 = A(x3 + x2 + x + 1) + B(x3 - x2 + x - 1) + (Cx3 - Cx + Dx2 - D)
⇒ 1 = (A + B + C)x3 + (A - B + D)x2 + (A + B - C)x + A - B - D
Comparing the coefficient of x3, x2, x and constant term in both side, we get
A + B + C = 0
A - B + D = 0
A + B - C = 0
and A - B - D = 1
Now, solving these equation, we get

Question 17.
Answer:
Let I = ∫ dx
Putting sin x= t
⇒ cos x dx = dt
∴
Let
⇒ 1 = A(2 - t) + B(1 - t)
⇒ 1 = 2A + B - (A + B)t
Equating the coefficients of f and constant terms of both sides, we get
A + B = 0 and 2A + B = 1
Now, solving these equations, we get
A = 1 and B = - 1
Question 18.
Answer:
Here, the given integral is improper rational function. Now putting x2 = y, we get
⇒ 4y + 10 = A(y + 4) + B(y + 3)
Putting y = - 3
4 × (- 3) + 10 = A(- 3 + 4)
⇒ - 12 + 10 = A
∴ A = - 2
Putting y = - 4
4(- 4) + 10 = B(- 4 + 3)
⇒ - 16 + 10 = - B
∴ B = 6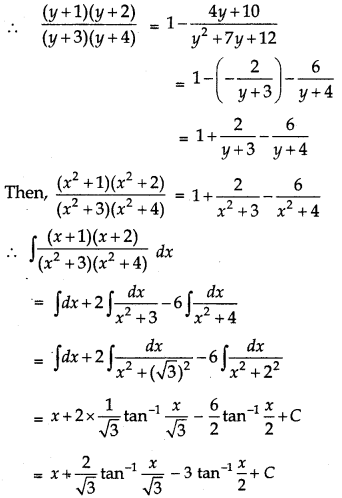
Question 19.
Answer:
Let I = ∫ dx
putting x2 = t
⇒ 2x dx = dt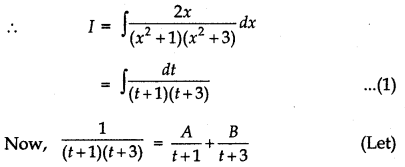
or 1 = A(t + 3) + B(t + 1)
1 = (A + B)t + 3A + B
Equating the coefficients of t and constant terms of both sides, we get
A + B = 0 and 3A + B = 1
Now, solving equations, we get
Question 20.
Answer:
Let I =
[Multiplying numerator and denominator by 4x3]
Putting x4 = t
⇒ 4x3 dx = dt
∴ I =
Now,
Equating the coefficients of t and constant terms of both sides, we get
A + B = 0, A = - 1
Question 21.
Answer:
Let I =
[Multiplying numerator and denominator by ex]
Putting ex = t ⇒ ex dx = dt.png)
Question 22.
∫ equals:
(A) log + C
(B) log + C
(C) log + C
(D) log |(x - 1) (x - 2)| + C
Answer:
Let
x = A(x - 2) + B(x - 1)
Putting x = 1
⇒ 1 = A(1 - 2) = - A
∴ A = - 1
Putting x = 2
⇒ 2 = B(2 - 1) = B
∴ B = 2
∴
∴ ∫
= - ∫ + 2 ∫
= - log |x - 1| + 2 log |x - 2| + C
= - log |x - 1| + log | (x - 2)2 | + C
= log + C
Hence, (B) is the correct answer.
Question 23.
∫ equals:
(A) log |x| - log |x2 + 1 | + C
(B) log |x| + log |x2 + 1| + C
(C) - log |x| + log |x2 + 1| + C
(D) log |x| + log |x2 + | + C
Answer:
Let I = ∫
= ∫ dx
[Multiplying numerator and denominator by x]
Putting x2 = t
⇒ 2x dx = dt ⇒ x dx = dt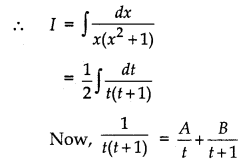
⇒ 1 = A(t + 1) + Bt
putting, t = 0
⇒ 1 = A(0 + 1) + B × 0 = A
∴ A = 1
Putting, t = - 1
⇒ 1 = B(- 1)
∴ B = - 1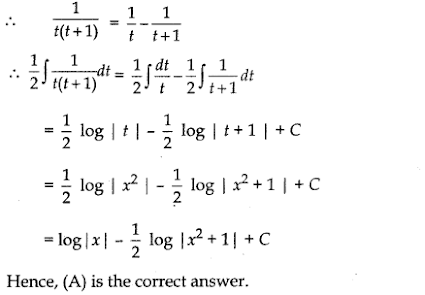






Either way the teacher or student will get the solution to the problem within 24 hours.