RBSE Class 12 Maths Solutions Chapter 7 Integrals Ex 7.4

 Question 1.

$\frac{3x^2}{x^6+1}$
Answer:

Question 2.
$\frac{1}{\sqrt{1+4x^2}}$
Answer:

Question 3.
$\frac{1}{\sqrt{(2-x{)}^2+1}}$
Answer:

Question 4.
$\frac{1}{\sqrt{9-25x^2}}$
Answer:

Question 5.
$\frac{3x}{1+2x^4}$
Answer:

Question 6.
$\frac{x^2}{1-x^6}$
Answer:

Question 7.
$\frac{x-1}{\sqrt{x^2-1}}$
Answer:

Question 8.
$\frac{x^2}{\sqrt{x^6+a^6}}$
Answer:

Question 9.
$\frac{{\sec }^{2}x}{\sqrt{{\tan }^{2}x+4}}$
Answer:
Let I = ∫$\frac{{\sec }^{2}x}{\sqrt{{\tan }^{2}x+4}}$ dx
Putting tan x = t
⇒ sec2 x dx = dt
∴ I = ∫$\frac{dt}{\sqrt{t^2+4}}$
= log |t + $\sqrt{t^2+4}$| + C
= log |tan x + $\sqrt{{\tan }^{2}x+4}$| + C

Question 10.
$\frac{1}{\sqrt{x^2+2x+2}}$
Answer:

Question 11.
$\frac{1}{9x^2+6x+5}$
Answer:

Question 12.
$\frac{1}{\sqrt{7-6x-x^2}}$
Answer:

Question 13.
$\frac{1}{\sqrt{(x-1)(x-2)}}$
Answer:
 

Question 14.

$\frac{1}{\sqrt{8+3x-x^2}}$
Answer:

Question 15.
$\frac{1}{\sqrt{(x-a)(x-b)}}$
Answer:

Question 16.
$\frac{4x+1}{\sqrt{2x^2+x-3}}$
Answer:

Question 17.
$\frac{x+2}{\sqrt{x^2-1}}$
Answer:

Question 18.
$\frac{5x-2}{1+2x+3x^2}$
Answer:
Let I = ∫$\frac{5x-2}{1+2x+3x^2}$ dx
Let A and B are two numbers such that:

5x - 2 = A $\frac{d}{dx}$ (1 + 2x + 3x2) + B
⇒ 5x - 2 = A(2 + 6x) + B
⇒ 5x - 2 = 6Ax + 2A + B
Comparing the coefficients of x and constant terms in both sides,

Question 19.
$\frac{6x+7}{\sqrt{(x-5)(x-4)}}$
Answer:
Let I = ∫$\frac{6x+7}{\sqrt{(x-5)(x-4)}}$ dx
= ∫$\frac{6x+7}{\sqrt{(x-5)(x-4)}}$ dx
Let A and B are two numbers such that:
6x + 7 = A $\frac{d}{dx}$(x2 - 9x + 20) + B
⇒ 6x + 7 = A(2x - 9) + B
⇒ 6x + 7 = 2A - 9A + B

Comparing the coefficients of x and constant terms in both sides, we get
2A = 6 and - 9A + B = 7
A = 3 and - 27 + B = 7 ⇒ B = 27 + 7 = 34

Question 20.
$\frac{x+2}{\sqrt{4x-x^2}}$
Answer:

Question 21.
$\frac{x+2}{\sqrt{x^2+2x+3}}$
Answer:

Question 22.
$\frac{x+3}{x^2-2x-5}$
Answer:

Question 23.
∫$\frac{5x+3}{\sqrt{x^2+4x+10}}$
Answer:
Let I = ∫$\frac{5x+3}{\sqrt{x^2+4x+10}}$ dx
Let A and B are two numbers such that:
5x + 3 = A $\frac{d}{dx}$ (x2 + 4x + 10) + B
⇒ 5x + 3 = A(2x + 4) + B
⇒ 5x + 3 = 2Ax + 4A + B

Comparing the coefficients of x and constant terms from both sides, we have

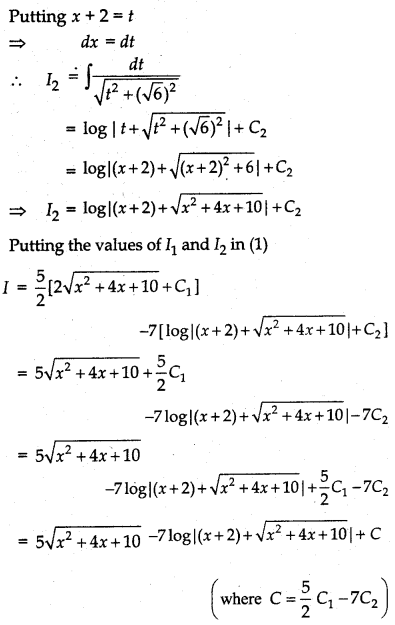
Question 24.
∫$\frac{dx}{x^2+2x+2}$ equals:
(A) x tan-1 (x + 1) + C
(B) tan-1 (x + 1) + C
(C) (x + 1) sin-1 x + C
(D) tan-1 x + C
Answer:
∫$\frac{dx}{x^2+2x+2}$ = ∫$\frac{dx}{x^2+2x+1+1}$
= ∫$\frac{dx}{(x+1{)}^2+1^2}$ = tan-1 $\left(\frac{x+1}{1}\right)$ + C
= tan-1 (x + 1) + C
Hence, (B) is the correct answer.

Question 25.
∫$\frac{dx}{\sqrt{9x-4x^2}}$ equals:
(A) $\frac{1}{9}{\sin }^{-1}\left(\frac{9x-8}{8}\right)+C$
(B) $\frac{1}{2}{\sin }^{-1}\left(\frac{8x-9}{9}\right)+C$
(C) $\frac{1}{2}{\sin }^{-1}\left(\frac{9x-8}{9}\right)+C$
(D) $\frac{1}{3}{\sin }^{-1}\left(\frac{9x-8}{9}\right)+C$
Answer:

Hence, (B) is the correct answer.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !