RBSE Class 12 Maths Solutions Chapter 7 Integrals Ex 7.3

 Question 1.

sin2 (2x + 5)
Answer:

Question 2.
sin 3x cos 4x
Answer:

Question 3.
cos 2x cos 4x cos 6x
Answer:
Let I = ∫cos 2x cos 4x cos 6x dx

Question 4.
sin3 (2x + 1)
Answer:

Question 5.
sin3 x cos3 x
Answer:
Let I = ∫ sin3 x cos3 x dx
= ∫sin x sin2 x cos3 x dx
= ∫sin x (1 - cos2 x) cos3 x dx
Putting cos x = t
⇒ - sin x dx = dt
⇒ sin x dx = - dt
∴ ∫sin x(1 - cos2 x) cos3 x dx
= - ∫(1 - t2) t3 dt
= - ∫ (t3 - t5) dt
= ∫t5 dt - ∫t3 dt
= $\frac{t^6}{6}-\frac{t^4}{4}$ + C
= $\frac{1}{6}$ cos6 x - $\frac{1}{4}$ cos4 x + C

Question 6.
sin x sin 2x sin 3x
Answer:
Let I = ∫sin x sin 2x sin 3x
= $\frac{1}{2}$ ∫2 sin x sin 2x sin 3x dx
[Multiplying numerator and denominator by 2]
= $\frac{1}{2}$ ∫ (2 sin x sin 2x) sin 3x dx
= $\frac{1}{2}$ ∫ [cos(x - 2x) - cos(x + 2x)] sin 3x dx
[∵ 2 sin A sin B = cos(A - B) - cos (A + B)]
= $\frac{1}{2}$ ∫ [cos (- x) - cos 3x] sin 3x dx
= $\frac{1}{2}$ ∫ (cos x - cos 3x) sin 3x dx [∵ cos (- θ) = cos θ)]
= $\frac{1}{2}$ ∫cos x sin x dx - $\frac{1}{2}$ ∫ cos 3x sin 3x dx
= $\frac{1}{4}$ ∫ 2 sin 3x cos x dx - $\frac{1}{4}$ ∫ 2 cos 3x sin 3x dx
[Multiplying numerator and denominator by 2]

Question 7.
sin 4x sin 8x
Answer:

Question 8.
$\frac{1-\cos x}{1+\cos x}$
Answer:
Let

Question 9.
$\frac{\cos x}{1+\cos x}$
Answer:

Question 10.
sin4 x
Answer:

Question 11.
cos4 2x
Answer:

Question 12.
$\frac{{\sin }^{2}x}{1+\cos x}$
Answer:
∫$\frac{{\sin }^{2}x}{1+\cos x}dx=\int \frac{1-{\cos }^{2}x}{1+\cos x}$ dx
= ∫ $\frac{(1-\cos x)(1+\cos x)}{(1+\cos x)}$ dx
= ∫ (1 - cos x) dx = ∫ dx - ∫ cos x dx
= x - sin x + C

Question 13.
$\frac{\cos 2x-\cos 2\alpha }{\cos x-\cos \alpha }$
Answer:

= 2 ∫ (cos x + cos α) dx
= 2 ∫ cos x dx + 2 ∫ cos α dx
= 2 sin x + 2x cos α + C
= 2(sin x + x cos α) + C

Question 14.
$\frac{\cos x-\sin x}{1+\sin 2x}$
Answer:

Question 15.
tan3 2x sec 2x
Answer:
Let I = ∫tan3 2x
= ∫tan2 2x.tan 2x sec 2x dx
= ∫ (sec2 2x - 1) tan 2x sec 2x dx
Putting sec 2x = t
⇒ 2 sec 2x tan 2x dx = dt
⇒ sec 2x tan 2x dx = $\frac{1}{2}$ dt

Question 16.
tan4 x
Answer:
Let I = ∫ tan4 x dx = ∫ tan2 x.tan2 x dx
= ∫ tan2 x (sec2 x - 1) dx
= ∫ tan2 x sec2 x dx - ∫ tan2 x dx
= ∫ tan2 x sec2 x dx - ∫ (sec2 x - 1) dx
= ∫ tan2 x sec2 x dx - ∫ (sec2 x - 1) dx
= ∫ tan2 x sec2 x dx - ∫ sec2 x dx + ∫ dx .......... (i)
Putting tan x = t
⇒ sec2 x dx = dt
∴ ∫ tan2 x sec2 x dx = ∫ t2 dt
= $\frac{t^3}{3}=\frac{{\tan }^{3}x}{3}$
From (i),
∴ ∫ tan2 x sec2 x dx - ∫ sec2 x dx + ∫ dx
= $\frac{{\tan }^{3}x}{3}$ - tan x + x + C
= $\frac{1}{3}$tan3 x - tan x + x + C

Question 17.
$\frac{{\sin }^{3}x+{\cos }^{3}x}{{\sin }^{2}x{\cos }^{2}x}$
Answer:

= ∫ sec x tan x dx + ∫cosec x cot x dx
= sec x - cosec x + C

Question 18.
$\frac{\cos 2x+2{\sin }^{2}x}{{\cos }^{2}x}$
Answer:

Question 19.
$\frac{1}{\sin x{\cos }^{3}x}$
Answer:

Question 20.
$\frac{\cos 2x}{(\cos x+\sin x{)}^2}$
Answer: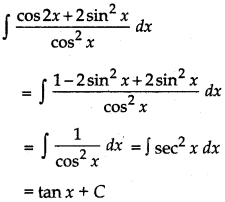

Question 21.
sin-1 (cos x)
Answer:

Question 22.
$\frac{1}{\cos (x-a)\cos (x-b)}$
Answer:

Question 23.
∫ $\frac{{\sin }^{2}x-{\cos }^{2}x}{{\sin }^{2}x{\cos }^{2}x}$ dx is equal to:
(A) tan x + cot x + C
(B) tan x + cosec x + C
(C) - tan x + cot x + C
(D) tan x + sec x + C
Answer:

= ∫ sec2 x dx - ∫ cosec2 x dx
= tan x + cot x + C
Hence, (A) is the correct answer.

Question 24.
∫ $\frac{e^x(1+x)}{{\cos }^2\left(e^{x}x\right)}$ dx equals:
(A) - cot (exx) + C
(B) tan (xex) + C
(C) tan (ex) + C
(D) cot (ex) + C
Answer:
∫ $\frac{e^x(1+x)}{{\cos }^2\left(e^{x}x\right)}$ dx
Putting ex x = t
⇒ (xex + ex) dx = dt
⇒ ex (1 + x) dx = dt
∴ ∫$\frac{e^x(1+x)}{{\cos }^2\left(e^{x}x\right)}$ dx = ∫$\frac{dt}{{\cos }^{2}t}$
= ∫ sec2 t dt
= tan t + C
= tan (exx) + C
Hence, (B) is correct answer.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !