RBSE Class 12 Maths Solutions Chapter 7 Integrals Ex 7.2

RBSE Class 12 Maths Solutions Chapter 7 Integrals Ex 7.2

Question 1.

$\frac{2x}{1+x^2}$
Answer:
Let I = ∫ $\frac{2x}{1+x^2}$ dx
Putting 1 + x2 = t
⇒ 2x dx = dt
∴ ∫ $\frac{2x}{1+x^2}$ dx = ∫ $\frac{dt}{t}$
= log |t| + C
= log |1 + x2| + C
= log (1 + x2) + C

Question 2.

$\frac{(\log x{)}^2}{x}$
Answer:

Question 3.
$\frac{1}{(x+x\log x)}$
Answer:

Question 4.
sin x sin (cos x)
Answer:
Let I = ∫sin x sin (cos x) dx
Putting cos x = t
⇒ - sin x dx = dt
⇒ sin x dx = - dt
∴ ∫ sin x sin (cos x) dx = - ∫ sin t dt
= + cos t + C
= cos (cos x) + C

Question 5.

sin (ax + b) cos (ax + b)
Answer:
Let I = ∫ sin (ax + b) cos (ax + b) dx
Putting sin (ax + b) = t
⇒ a cos (ax + b) dx = dt
⇒ cos (ax + b) dx = $\frac{dt}{a}$

Remark : Here, we can also evaluate integral by assuming cos (ax + b) = t.
Putting cos(ax + b) = t
⇒ - a sin(ax + b) dx = dt
⇒ sin (ax + b) dx = - $\frac{dt}{a}$
∴ ∫sin (ax + b) cos(ax + b)dx
= - $\int \frac{tdt}{a}=-\frac{1}{a}\int t$ dt
= - $\frac{1}{a}\cdot \frac{t^2}{2}$ + C
= - $\frac{{\cos }^2(ax+b)}{2a}$ + C

Second Method:
∫ sin (ax + b) cos (ax + b) dx
= $\frac{1}{2}$ ∫ 2 sin (ax + b) cos (ax + b) dx
[Multiplying numerator and denominator by 2]
= $\frac{1}{2}$ ∫ sin 2(ax + b) dx
= $\frac{1}{2}$ ∫ sin (2ax + 2b) dx
Putting 2ax + 2b = t
⇒ 2a dx = dt

Question 6.
x$\sqrt{ax+b}$
Answer:
Let I = ∫ $\sqrt{ax+b}$ dx = ∫ (ax + b)1/2 dx
Putting ax + b = t
⇒ a dx = dt
⇒ dx = 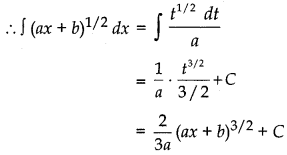$\frac{dt}{a}$

Question 7.
x$\sqrt{x+2}$
Answer:

Question 8.
x$\sqrt{1+2x^2}$
Answer:
Let I = ∫ x$\sqrt{1+2x^2}$ dx
Putting 1 + 2x2 = t
⇒ 4 dx = dt
⇒ x dx = $\frac{dt}{4}$

Question 9.
(4x + 2) $\sqrt{x^2+x+1}$
Answer:

Question 10.
$\frac{1}{x-\sqrt{x}}$
Answer:

Question 11.
$\frac{x}{\sqrt{x+4}}$, x > 0
Answer:
Let I = ∫ $\frac{x}{\sqrt{x+4}}$ dx
Putting x + 4 = t
⇒ dx = dt
and x = t - 4

Question 12.
(x3 - 1)1/3 x5
Answer:
Let I = ∫ (x3 - 1)1/3 x5
Putting x3 - 1 = t
⇒ 3x2 dx = dt
⇒ x2 dx = $\frac{dt}{3}$
and x3 = t + 1
∴ ∫ (x3 - 1)1/3 x5 dx = ∫ (x3 - )1/3 . x3 .x2 dx

Question 13.
$\frac{x^2}{{(2+3x^3)}^3}$
Answer:
Let I = ∫ $\frac{x^2}{{(2+3x^3)}^3}$ dx
Putting 2 + 3x3 = t
⇒ 9x2 dx = dt
⇒ x2 dx = $\frac{1}{9}$ dt

Question 14.
$\frac{1}{x(\log x{)}^m}$, x > 0 , m ≠ 1
Answer:

Question 15.
$\frac{x}{9-4x^2}$
Answer:
Let I = ∫ $\frac{x}{9-4x^2}$ dx
Putting 9 - 4x2 = t
⇒ - 8x dx = dt
⇒ x dx = - $\frac{1}{8}$dt

Question 16.
e2x + 3
Answer:
Let I = ∫ e2x + 3 dx
= ∫ e2x . e3 dx
= e3 ∫ e2x dx
Putting 2x = t
⇒ 2 dx = dt
⇒ dx = $\frac{dt}{2}$
∴ ∫ e2x + 3 dx = e3 ∫ et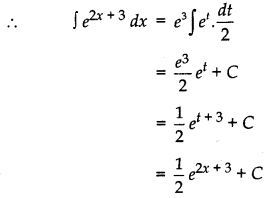

Alter: ∫ e2x + 3 dx
Let 2x + 3 = t
2 dx = dt
or dx = $\frac{dt}{2}$
∴ ∫ e2x + 3 dx = $\frac{1}{2}$ ∫ et dt = $\frac{1}{2}$ et + C
= $\frac{1}{2}$ e2x + 3 + C

Question 17.

$\frac{x}{e^{x^2}}$
Answer:

Question 18.
$\frac{e^{{\tan }^{-1}x}}{1+x^2}$
Answer:

Question 19.
$\frac{e^{2x}-1}{e^{2x}+1}$
Answer:

Question 20.
$\frac{e^{2x}-e^{-2x}}{e^{2x}+e^{-2x}}$
Answer:
Let I = $\frac{e^{2x}-e^{-2x}}{e^{2x}+e^{-2x}}$
Putting e2x + e-2x = t
⇒ (2e2x - 2e-2x) dx = dt
⇒ (e2x - e-2x) = $\frac{1}{2}$ dt
∴ ∫$\frac{e^{2x}-e^{-2x}}{e^{2x}+e^{-2x}}$ dx = $\frac{1}{2}\int \frac{1}{t}$ dt
= log |t| + C
= log |e2x + e-2x| + C

Question 21.
tan2 (2x - 3)
Answer:
Let I = ∫ tan2 (2x - 3) dx
= ∫ {sec2 (2x - 3) - 1} dx
= ∫ sec2 (2x - 3) dx - ∫ dx
Putting 2x - 3 = t
⇒ 2dx = dt
⇒ dx = $\frac{1}{2}$dt
∴ ∫ tan2 (2x - 3) dx = ∫ sec2 (2x - 3) dx = ∫ dx
= $\frac{1}{2}$ ∫ sec2 t.dt - ∫ dx
= $\frac{1}{2}$ tan t - x + C
= $\frac{1}{2}$ tan (2x - 3) - x + C

Question 22.
sec2 (7 - 4x)
Answer:
Let I = ∫ sec2 (7 - 4x) dx
Putting 7 - 4x = t
⇒ - 4 dx = dt
⇒ dx = - $\frac{1}{4}$ dt
∴ ∫ sec2 (7 - 4x) dx = - $\frac{1}{4}$ ∫sec2 t dt
= - $\frac{1}{4}$ tan t + C
= - $\frac{1}{4}$ tan (7 - 4x) + C

Question 23.
$\frac{{\sin }^{-1}x}{\sqrt{1-x^2}}$
Answer:
Let I = ∫ $\frac{{\sin }^{-1}x}{\sqrt{1-x^2}}$ dx
Putting sin-1 x = t

Question 24.
$\frac{2\cos x-3\sin x}{6\cos x+4\sin x}$
Answer: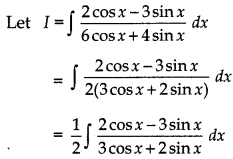

Putting 3 cos x + 2 sin x = t
⇒ (- 3 sin x + 2 cos x) dx = dt
⇒ (2 cos x - 3 sin x) dx = dt

Question 25.
Answer:

Question 26.
$\frac{\cos \sqrt{x}}{\sqrt{x}}$
Answer:

Question 27.
$\sqrt{\sin 2x}$ cos 2x
Answer:
Let I = ∫ $\sqrt{\sin 2x}$ cos 2x dx
Putting sin 2x = t
⇒ 2 cos 2x dx = dt
⇒ cos 2x dx = $\frac{1}{2}$ dt

Question 28.
$\frac{\cos x}{\sqrt{1+\sin x}}$
Answer:

Question 29.
cot x log sin x
Answer:
Let I = ∫ cot x log sin x dx
Putting log sin x = t
⇒ $\frac{1}{\sin x}$ × cos x dx = dt
⇒ cot x dx = dt
∴ ∫ cot x (log sin x) dx = ∫t dt = $\frac{t^2}{2}$ + C
= $\frac{(\log \sin x{)}^2}{2}$ + C

Question 30.

$\frac{\sin x}{1+\cos x}$
Answer:
Let I = ∫ $\frac{\sin x}{1+\cos x}$ dx
Putting 1 + cos x = t
⇒ - sin x dx = dt
⇒ sin x dx = - dt
∴ ∫ $\frac{\sin x}{1+\cos x}$ dx = - ∫ $\frac{1}{t}$ dt
= - log |t| + C
= - log |(1 + cos x)| + C

Question 31.
$\frac{\sin x}{(1+\cos x{)}^2}$
Answer:
Let I = ∫ $\frac{\sin x}{(1+\cos x{)}^2}$ dx
Putting 1 + cos x = t
⇒ - sin x dx = dt
⇒ sin x dx = - dt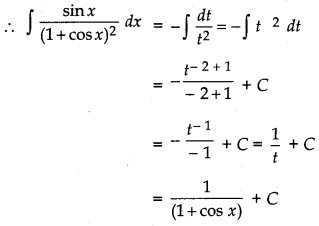

Question 32.
$\frac{1}{(1+\cot x)}$
Answer:

Question 33.
$\frac{1}{1-\tan x}$
Answer:

Question 34.
$\frac{\sqrt{\tan x}}{\sin x\cos x}$
Answer:

Question 35.
$\frac{(1+\log x{)}^2}{x}$
Answer:

Question 36.
$\frac{(x+1)(x+\log x{)}^2}{x}$
Answer:

Question 37.
$\frac{x^3\sin \left({\tan }^{-1}{x}^4\right)}{1+x^8}$
Answer:

Question 38.
∫ $\frac{10x^9+{10}^x{\log }_{e}10}{x^{10}+{10}^x}$ dx equals:
(A) 10x - x10 + C
(B) 10x + x10 + C
(C) (10x - x10)-1
(D) log (10x + x10) + C
Answer:
Let x10 + 10x = t
⇒ (10x9 + 10x loge 10) dx = dt
∴ ∫ $\frac{10x^9+{10}^x{\log }_{e}10}{x^{10}+{10}^x}$ dx = ∫$\frac{dt}{t}$
= log |t| + C
= log (x10 + 10x) + C
Hence, (D) is the correct answer.

Question 39.

∫ $\frac{dx}{{\sin }^{2}x{\cos }^{2}x}$ equals:
(A) tan x + cot x + C
(B) tan x - cot x + C
(C) tan x cot x + C
(D) tan x - cot 2x + C
Answer:

Hence, (B) is the correct answer.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !