RBSE Class 12 Maths Solutions Chapter 7 Integrals Ex 7.1

RBSE Class 12 Maths Solutions Chapter 7 Integrals Ex 7.1

Question 1.

sin 2x
Answer:
Let I = ∫ sin 2x dx
We know that
$\frac{d}{dx}$ (cos 2x) = - 2 sin 2x
⇒ $\frac{d}{dx}$ (-$\frac{1}{2}$cos 2x) = sin 2x
∴ ∫sin 2x dx = - $\frac{1}{2}$ cos 2x + C

Question 2.
cos 3x
Answer:
Let I = cos 3x
We know that
$\frac{d}{dx}$ (sin 3x) = 3 cos 3x
⇒ $\frac{d}{dx}$ (-$\frac{1}{3}$sin 3x) = cos 3x
∴ ∫cos 3x dx = - $\frac{1}{3}$ sin 3x + C

Question 3.
e2x
Answer:
Let I = ∫e2x dx
We know that

Question 4.
(ax + b)2
Answer:
Let I = ∫(ax + b)2 dx
We know that

Question 5.

sin 2x - 4e3x
Answer:
Let I = ∫ (sin 2x - 4e3x) dx
= ∫ sin 2x dx - 4 ∫e3x dx

Question 6.
∫ (4e3x + 1) dx
Answer:
∫ (4e3x + 1) dx = 4 ∫e3x dx + ∫ 1 dx
= 4 $\frac{e^{3x}}{3}$ + x + C
= $\frac{4}{3}$ e3x + x + C

Question 7.
∫x2$(1-\frac{1}{x^2})$ dx
Answer:
Let I = ∫x2$(1-\frac{1}{x^2})$dx
= ∫ (x2 - 1) dx
= ∫ x2 dx - ∫ 1 dx
= $\frac{x^3}{3}$ - x + C

Question 8.
∫ (ax2 + bx + c) dx
Answer:
∫ (ax2 + bx + c) dx
= a ∫x2 dx + b ∫ x dx + c ∫ 1.dx

Question 9.
∫ (2x2 + ex) dx
Answer:
∫ (2x2 + ex) dx = 2 ∫ x2 dx + ∫ ex dx
= 2$\frac{x^{2+1}}{2+1}$ + ex + C
= $\frac{2}{3}$x3 + ex + C

Question 10.
∫ ${(\sqrt{x}-\frac{1}{\sqrt{x}})}^2$ dx
Answer:

Question 11.
∫ $\frac{x^3+5x^2-4}{x^2}$ dx
Answer:

Question 12.
∫$\frac{x^3+3x+4}{\sqrt{x}}$ dx
Answer:

Question 13.
∫$\frac{x^3-x^2+x-1}{x-1}$ dx
Answer:

Question 14.
∫ (1 - x) √x dx
Answer:
∫ (1 - x) √x dx = ∫(√x - x√x)dx
= ∫ (x1/2 - x.x1/2) dx
= ∫ x1/2 dx - ∫ x3/2 dx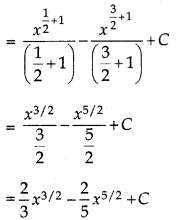

Question 15.
∫ √x(3x2 + 2x + 3) dx
Answer:

Question 16.
∫ (2x - 3 cos x + ex) dx
Answer:
∫ (2x - 3 cos x + ex) dx
= 2 ∫x dx - 3 ∫ cos x dx + ∫ ex dx
= 2.$\frac{x^2}{2}$ - 3 sin x + ex + C
= x2 - 3 sin x + ex + C

Question 17.
∫ (2x2 - 3 sin x + 5√x) dx
Answer:
∫ (2x2 - 3 sin x + 5√x) dx
= 2 ∫x2 dx - 3 ∫ sin x dx + 5 ∫x1/2 dx

Question 18.
∫ sec x (sec x + tan x) dx
Answer:
∫ sec x (sec x + tan x) dx
= ∫ sec2x dx + ∫sec x tan x dx
= tan x + sec x + C

Question 19.
∫ $\frac{{\sec }^{2}x}{{cosec}^{2}x}$
Answer:
Let I = ∫$\frac{{\sec }^{2}x}{{cosec}^{2}x}$ dx = ∫$\frac{{\sin }^{2}x}{{\cos }^{2}x}$ dx
= ∫tan2 dx
= ∫ (sec2 x - 1) dx
= ∫ sec2 x dx - ∫1. dx
= tan x - x + C

Question 20.
∫$\frac{2-3\sin x}{{\cos }^{2}x}$ dx
Answer:
Let I = ∫$\frac{2-3\sin x}{{\cos }^{2}x}$ dx
= ∫$\frac{2}{{\cos }^{2}x}dx-3\int \frac{\sin x}{{\cos }^{2}x}$ dx
= 2 ∫ sec2 x dx - 3 ∫ sec x tan x dx
= 2 tan x - 3 sec x + C

Question 21.

The antiderivative of (√x + $\frac{1}{\sqrt{x}}$) equals:
(A) $\frac{1}{3}$x1/3 + 2x1/2 + C
(B) $\frac{2}{3}$x2/3 + $\frac{1}{2}$x2 + C
(C) $\frac{2}{3}$x3/2 + 2x1/2 + C
(D) $\frac{3}{2}$x3/2 + $\frac{1}{2}$x1/2 + C
Answer:

Hence, (C) is the correct answer.

Question 22.
If $\frac{d}{dx}$ f(x) = 4x3 - $\frac{3}{x^4}$ such that f(2) = 0. Then f(x) is:
(A) $x^4+\frac{1}{x^3}-\frac{129}{8}$
(B) $x^3+\frac{1}{x^4}+\frac{129}{8}$
(C) $x^4+\frac{1}{x^3}+\frac{129}{8}$
(D) $x^3+\frac{1}{x^4}-\frac{129}{8}$
Answer:

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !