RBSE Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.4

 Question 1.

Using differentials, find the approximate value of each of the following upto 3 places of decimal.
(i) √25.3
Answer:

(ii) √49.5
Answer: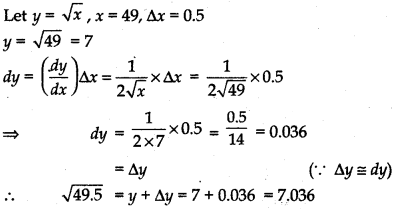

(iii) √0.6
Answer:
Let y = √x, x = 0.64, y = 0.8
Δx = 0.6 - 0.64 = - 0.04

(iv) (0.009)1/3
Answer:
Let y = x1/3 and x = 0.008
Δx = 0.009 - 0.008 = 0.001

(v) (0.999)1/10
Answer:

(vi) (15)1/4
Answer:

(vii) (26)1/3
Answer:
We know that (27)1/3 = 3
Let y = x1/3, x = 27, y = 3, Δx = 1

= - 0.037037 = Δy (∵ Δy ≅ dy)
∴ (26)1/3 = y + Δy = 3 + (- 0.037037)
= 3 - 0.037037 = 2.962963 ≈ 2.963

(viii) (255)1/4
Answer:

(ix) (82)1/4
Answer:

(x) (401)1/2
Answer:

(xi) (0.0037)1/2
Answer:

(xii) (26.57)1/3
Answer:

(xiii) (81.5)1/4
Answer:

(xiv) (3.968)3/2
Answer:

(xv) (32.15)1/5
Answer:

Question 2.
Find the approximate value of f(2.01), where f(x) = 4x2 + 5x + 2.
Answer:
Given, f(x) = 4x2 + 5x + 2
f(2) = 4(2)2 + 5 × 2 + 2 = 28
∆x = 2.01 - 2 = 0.01
f’(x) = 8x + 5
df(x) = f’(x) × ∆x = (8x + 5) × ∆x
= (8 × 2 + 5) × 0.01 = (16 + 5) × 0.01
= 21 × 0.01 = 0.21
∴ f(2.01) = f(2) + df(x)
= 28 + 0.21 = 28.21

Question 3.
Find the approximate value of f(5.001), where f(x) = x3 - 7x2 + 15.
Answer:
Given, f(x) = x3 - 7x2 + 15
then f(5) = 53 - 7 × (5)2 + 15 = 125 - 7 × 25 + 15
= 125 - 175 + 15 = - 35
∆x = 5.001 - 5 = 0.001
f’(x) = 3x2 - 14x
df(x) = f’(x) × ∆x = (3x2 - 14x) ∆x
= (3 × 52 - 14 × 5) 0.001
⇒ df(x) = (75 - 70) × 0.001 = 5 × 0.001 = 0.005
∴ f(5.001) = f(5) + df(x) = - 35 + 0.005 = - 34.995

Question 4.
Find the approximate change in the volume V of a cube of side x metres caused by increasing the side by 1%.
Answer:
Let V be the volume of cube of side x metres.
Then V = x3
∴ $\frac{dV}{dx}$ = 3x2
We have, ∆x = $\frac{1}{100}$ × x = 0.01 x
Approximate increase in volume
dV = $\frac{dV}{dx}$ × ∆x = 3x2 × 100 = 0.03x3 m3
∴ Percentage increase in volume
= $\frac{dV}{dx}$ × 100 = $\frac{0.03x^3}{x^3}$ × 100 = 3%
Thus, approximate percentage increase in volume of cube = 3%

Question 5.
Find the approximate change in the surface area of a cube of side x metres caused by decreasing the side by 1%.
Answer:
Let S be surface area of cube.
∴ S = 6x2
Then $\frac{dS}{dx}$ = 12x
Decrease in side of cube = 1% of x = $\frac{1}{100}$ × x = 0.01x
Change in surface area = dS = $\frac{dS}{dx}$ × ∆x
= 12x × (0.01x) = 0.012x2 m2
Percentage change in surface area
= $\frac{dS}{S}$ × 100 = $\frac{0.12x^2}{6x^2}$ × 100 = 2%
Hence, percentage decrease in surface area = 2%

Question 6.
If the radius of a sphere is measured as 7 m with an error of 0.02 m, then find the approximate error in calculating its volume.
Answer:
We have, radius of sphere r 7 m
∆r = Error in measurement of radius = 0.02 m
Volume of sphere V = $\frac{4}{3}$πr3
∴ $\frac{dV}{dr}$ = $\frac{4}{3}$ × 3πr2 = 4πr2
∴ Error in measurement of volume of sphere
dV = $\frac{dV}{dr}$ × (∆r) = 4πr2 × ∆r
∴ dV = 4π × 49 × 0.02 = 3.92π m3

Question 7.
If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating its surface area.
Answer:
Radius of sphere r = 9 m
Error in radius = 0.03 m = ∆r
Surface area of sphere, S = 4πr2
⇒ $\frac{dS}{dr}$ = 4π × 2r = 8πr
Error in measurement of surface area
dS = $\frac{dS}{dr}$ × ∆r = 8πr × ∆r
∴ dS = 8π × 9 × 0.03 = 2.16π m2

Question 8.
If f(x) = 3x2 + 15x + 5, then approximate value of f(3.02) is:
(A) 47.66 (B) 57.66
(C) 67.66 (D) 77.66
Answer:
Given, f(x) = 3x2 + 15x + 5
x = 3
∆x = 3.02 - 3 = 0.02
⇒ f’(x) = 6x + 15
and f(3) = 3 × 32 + 15 × 3 + 5
= 3 × 9 + 45 + 5
= 27 + 45 + 5 = 77
df(x) = f’(x).∆x
x = 3
= (6x + 15) × (0.02)
= (6 × 3+ 15) × 0.02
= (18 + 15) × 0.02
= 33 × 0.02 = 0.66
∴ f(3.02) = f(3) + df(x)
= 77 + 0.66 = 77.66
Thus, (D) is correct.

Question 9.
The approximate change in the volume of a cube of side x metres caused by increasing the side by 3% is:
(A) 0.06 x3 m3
(B) 0.6 x3 m3
(C) 0.09 x3 m3
(D) 0.9 x3 m3
Answer:
Volume of cube V = x3
Increase in side = 3% of x
∴ ∆x = $\frac{3}{100}$ × x = 0.03x
∵ $\frac{dV}{dx}$ = 3x2
∴ Increase in volume = $\frac{dV}{dx}$ × ∆x
dV = 3x2 × 0.03x
∴ dV = 0.09x3 m3
Thus, (C) is correct.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !