RBSE Class 12 Maths Solutions Chapter 6 Application of Derivatives Ex 6.2

RBSE Class 12 Maths Solutions Chapter 6 Application of Derivatives Ex 6.2

Question 1.

Show that the function given by f(x) = 3x + 17 is increasing on R.
Answer:
Given,
f(x) = 3x + 17
Let x1, x2 ∈ R such that x1 < x2
3x1 < 3x2
3x1 + 17 < 3x2 + 17
f(x1) < f(x2)
∴ x1 < x2
f(x1) < f(x2)
Thus, f(x) = 3x + 17, is strictly increasing at R.
Hence Proved.

Question 2.

Show that the function given by .f(x) = e2x is increasing on R.
Answer:
Given, f(x) = e2x
∴ f'(x) = 2e2x
For ∀ x ∈ R, f'(x) > 0
Since 2 > 0, e2x > 0
Thus, function f, is strictly increasing at R.
Hence Proved.

Question 3.
Show that the function given by f(x) = sin x is
(a) increasing in $(0,\frac{\pi }{2})$
(b) decreasing in $(0,\frac{\pi }{2})$
(c) neither increasing nor decreasing in (0, π)
Answer:
Given, f(x) = sin x
⇒ f’(x) = cos x

(a) For interval $(0,\frac{\pi }{2})$
f’(x) = cos x > 0
∴ In x ∈ $(0,\frac{\pi }{2})$ f’(x) is positive.
Thus, f is strictly increasing in interval $(0,\frac{\pi }{2})$.
Hence Proved.

(b) In interval $(\frac{\pi }{2},\pi )$
f’(x) = cos x < 0 ⇒ f’(x) < 0
∴ In x ∈ $(\frac{\pi }{2},\pi )$, f’(x) < 0
Thus, function is strictly decreasing in interval $(\frac{\pi }{2},\pi )$.
Hence Proved.

(c) In interval (0, π),
f’(x) is not continuous +ve or -ve because in $(0,\frac{\pi }{2})$
f'(x) positive f’(x) > 0 and $(\frac{\pi }{2},\pi )$
f’(x) negative {f’(x) < 0}.
Thus, f, is neither increasing nor decreasing in interval (0, π).
Hence Proved.

Question 4.
Find the intervals in which the function f given by f(x) = 2x2 - 3x is:
(a) increasing (b) decreasing
Answer:
Here f(x) = 2x2 - 3x
∴ f’(x) = 4x - 3
f'(x) = 0, then 4x - 3 = 0
∴ x = 3/4
Thus, point x = 3/4 divides real number line into two disjoint intervals $(-\infty ,\frac{3}{4})$ and $(-\infty ,\frac{3}{4})$.

(a) In interval 

$(\frac{3}{4},\infty )$, f’(x) = positive
For x = 1 f’(x) = 4 - 3 = 1 > 0
∴ f is stricly increasing.
Thus, function is strictly increasing in interval $(\frac{3}{4},\infty )$.

(b) In interval $(-\infty ,\frac{3}{4})$, f’(x) negative
For x = - 1, f’(x) = - 4 - 3 = - 7 < 0
∴ f is strictly decreasing function.
Thus, function is strictly decreasing in interval $(-\infty ,\frac{3}{4})$

Question 5.
Find the intervals in which the function f given by f(x) = 2x3 - 3x2 - 36x + 7 is
(a) Increasing
(b) decreasing
Answer:
Given, f(x) = 2x3 - 3x2 - 36x + 7
⇒ f’(x) = 6x2 - 6x - 36
f’(x) = 0
⇒ 6x2 - 6x - 36 = 0
⇒ 6(x2 - x - 6) = 0
⇒ 6(x - 3) (x + 2) = 0
Either x - 3 = 0 or x + 2 = 0
⇒ x = 3 or x = - 2
Points x = - 2, x = 3 divide real number line into three disjoint intervals namely (- ∞, - 2), (- 2, 3) and (3, ∞).

(a) For interval (- ∞, - 2)
f’(x) = 6x2 - 6x - 36 > 0
Since, at x = - 3
f’(x) = 6(- 3)2 - 6(- 3) - 36
= 6 × 9 + 6 × 3 - 36
= 54 + 18 - 36
= 36 > 0
Similarly, we can prove f(x) > 0 for n ∈ (- ∞, - 2).
Thus, in (- ∞ - 2) function is strictly increasing i.e., for x ∈ (- ∞, - 2) function is strictly increasing.

(b) For interval (- 2, 3)
f’(x) = 6x2 - 6x - 36 < 0
Since, at x = 1,
f’(x) = 6(1)2 - 6 × 1 - 36
= 6 - 6 - 36
= - 36 < 0
At x = 0, f’(x) = 6(0)2 - 6 × 0 - 36
= - 36 < 0
Similarly, we can prove f’(x) < 0.
For x ∈ (- 2, 3) function is strictly decreasing.

(c) For interval (3, ∞)
f’(x) = 6x2 - 6x - 36 > 0
Since, at x = 4,
f’(x) = 6 × (4)2 - 6 × 4 - 36
= 96 - 24 - 36
= 96 - 60
= 36 > 0
At x = 5,
f’(x) = 6(5)2 - 6 × 5 - 36
= 6 × 25 - 30 - 36
= 150 - 30 - 36 = 84 > 0
Similarly, we can show for other points that f’(x) > 0. Thus, for x ∈ (3, ∞), function is strictly increasing hence, function f is strictly increasing in interval:
(- ∞ - 2) ∪ (3, ∞) f{f'(x) > 0}
In interval (- 2, 3), function strictly decreasing f{f'(x) < 0}.

Question 6.
Find the intervals in which the following functions are strictly increasing or decreasing:
(a) f(x) = x2 + 2x + 5
Answer:
Given, f(x) = x2 + 2x + 5
⇒ f’(x) = 2x + 2
f’(x) = 0 ⇒ 2x + 2 = 0
⇒ 2(x + 1) = 0 ⇒ x + 1 = 0 ⇒ x = - 1
Point x = - 1 divides real number line into two disjoint intervals namely (- ∞, - 1) and (- 1, ∞).

(i) In interval (- ∞, - 1)
f’(x) = 2(x + 1) < 0
Since, in x ∈ (- ∞, - 1), x < 0
For x = - 2
f’(x) = 2(- 2 + 1) = 2(- 1) = - 2 < 0
For x = - 3
f’(x) = 2(- 3 + 1) = 2(- 2) = - 4 < 0 Similarly, it can be shown for other points also. Thus, for x ∈ (- ∞, - 1), function is strictly decreasing.

(ii) For interval (- 1, ∞), f’(x) = 2(x + 1) > 0
Since x > - 1
For x = 0
f’(x) = 2(0 + 1) - 2 × 1 = 2 > 0
For x = 1
f’(x) = 2(1 + 1) = 2 × 2 = 4 > 0
Similarly, it can be shown for other points also.
Thus, for x ∈ (- 1, ∞), function f is strictly increasing.

(b) f(x) = 10 - 6x - 2x2
Answer:
Given, f(x) = 10 - 6x - 2x2
⇒ f’(x) = - 6 - 4x = - 2(3 + 2x)
f’(x) = 0 ⇒ - 2(3 + 2x) = 0
⇒ 3 + 2x = 0 ⇒ x = -$\frac{3}{2}$
Point x = -$\frac{3}{2}$ divides real number line into two disjoints intervals namely (- ∞, - $\frac{3}{2}$) and (- $\frac{3}{2}$, ∞).

(i) For interval $(-\infty ,-\frac{3}{2})$
f’(x) = - 2(3 + 2x) > 0
For x = - 2
f’(x) = - 2{3 + 2(- 2)) = - 2(3 - 4)
= - 2(- 1) = 2 > 0
For x = - 3
f’(x) = - 2{3 + 2(- 3)} = - 2(3 - 6)
= - 2(- 3) = 6 > 0
Similarly, it can be shown for other points also that f’(x) > 0
Thus, for x ∈ (- ∞, -$\frac{3}{2}$), function f is strictly increasing.

(ii) For interval $(-\frac{3}{2},\infty )$
f’(x) = - 2(3 + 2x) < 0
For x = - 1,
f(x) = - 2{3 + 2(- 1)1 = - 2(3 - 2)
= - 2 × 1 = - 2 < 0
For x = 0
f’(x) = - 2(3 + 2 × 0)
= - 2 × 3 = - 6 < 0
For x = 1,
f’(x) = - 2(3 + 2 × 1) = - 2(3 + 2)
= - 2 × 5 = - 10 < 0
Similarly, it can be shown for other points also.
Thus for x ∈ $(-\frac{3}{2},\infty )$ function f is strictly decreasing.

(c) f(x) = - 2x3 - 9x2 - 12x + 1
Answer:
Given, f(x) = - 2x3 - 9x2 - 12x + 1
⇒ f’(x) = - 6x2 - 18x - 12 = - 6(x2 + 3x + 2)
f(x) = 0 ⇒ - 6(x2 + 3x + 2) = 0
Either x + 2 = 0 or x + 1 = 0
= x = - 2 or x = - 1
Points x = - 2 and x = - 1 divide real number line into three intervals namely (- ∞, - 2), (- 2, - 1) and (- 1, ∞).

(i) For interval (- ∞, - 2)
f’(x) = - 6(x2 + 3x + 2) < 0
For x = - 3
f’(x) = 6{(- 3)2 + 3(- 3) + 21
= - 6(9 - 9 + 2) = - 12 < 0
For x = - 4
f’(x) = - 6{(- 4)2 + 3(- 4) + 2}
= - 6(16 - 12 + 2) - 36 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ (- ∞, - 2) function is strictly decreasing.

(ii) For interval (- 2, - 1)
f’(x) = - 6(x2 + 3x + 2) > 0
For x = - 1.5
f’(x) = - 6{(- 1.5)2 + 3(- 1.5) + 2)}
= - 6(2.25 - 4.5 + 2)
= + 1.50 > 0
Similarly, by taking another point we can show that f’(x) > 0.
Thus, f for x ∈ (- 2, - 1) function is strictly increasing.

(iii) For interval (- 1, ∞)
f’(x) = - 6(x2 + 3x + 2) < 0
For x = 0
f’(x) = - 6(02 + 3 × 0 + 2)
= - 6 × 2 = - 12 < 0
For x = 1
f’(x) = - 6{(1)2 + 3 × 1 + 2}
= - 6(1 + 3 + 2) = - 36 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ (- 1, ∞) function f is strictly decreasing.
Thus, by (i) and (iii) we can say that function is strictly decreasing in (- ∞, - 2) ∪ (- 1, ∞).

(d) f(x) = 6 - 9x - x2
Answer:
Given, f(x) = 6 - 9x - x2
⇒ f’(x) = - 9 - 2x
f’(x) = 0 ⇒ - 9 - 2x = 0
⇒ - 2x = 9 ⇒ x = -$\frac{9}{2}$
Point x = -$\frac{9}{2}$ divides real number line into two disjoints intervals namely $(-\infty ,-\frac{9}{2})$ and $(-\frac{9}{2},\infty )$.

(i) For $(-\infty ,-\frac{9}{2})$
f’(x) = - 9 - 2x > 0
For x = - 5
f’(x) = - 9 - 2(- 5) - 9 + 10 = 1 > 0
For x = - 6
f’(x) = - 9 - 2(- 6) = - 9 + 123 > 0
Similarly, by taking another points we can show that f’(x) > 0.
Thus, for x ∈ $(-\infty ,-\frac{9}{2})$, function f is strictly increasing.

(ii) For interval $(-\frac{9}{2},\infty )$
f’(x) = - 9 - 2x < 0
For x = - 4
f’(x) = - 9 - 2(- 4) - 9 + 8 - 1 < 0
For x = - 3
f’(x) = - 9 - 2(- 3) = - 9 + 6 = - 3 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ $(-\frac{9}{2},\infty )$ function f is strictly decreasing.

(e) f(x) = (x + 1)3 (x - 3)3
Answer:
Given, f(x) = (x + 1)3 (x - 3)3
⇒ f’(x) = (x + 1)3.$\frac{d}{dx}$f(x - 3)3 +(x - 3)3 $\frac{d}{dx}$ (x + 1)3
⇒ f’(x) = (x + 1)3.3(x - 3)3 + (x - 3)3.3(x + 1)2
⇒ f’(x) = 3(x + 1)2 (x - 3)2 [(x + 1 + x - 3)]
⇒ f’(x) = 3(x + 1)2 (x - 3)2 (2x - 2)
⇒ f’(x) = 3(x + 1)2 (x - 3)2 2(x —1)
⇒ f’(x) = 6(x -1) (x + 1)2 (x - 3)2
f’(x) = 0
⇒ 6(x - 1) (x + 1)2 (x - 3)2 = 0
⇒ x - 1 = 0 or (x + 1)2 = 0 or (x - 3)2 = 0
⇒ x = 1 or x = - 1 or x = 3
Points x = - 1, x = 1 and x = 3 divide real number line into four disjoint intervals namely (- ∞, - 1), (- 1, 1), (1, 3) and (3, ∞).

(i) For interval (- ∞ , - 1)
f’(x) = 6(x - 1) (x + 1)2 (x - 3)2 < 0
For x -2
f’(x) = 6(- 2 - 1) (- 2 + 1)2 (- 2 - 3)2
⇒ f’(x) = 6(- 3) (- 1)2 (- 5)2
⇒ f’(x) = - 18 × 1 × 25 = - 450 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ (- ∞, - 1), function f is strictly decreasing.

(ii) For interval (- 1, 1)
f’(x) = 6(x - 1) (x + 1)2 (x - 3)2 < 0
For x = 0
f’(x) = 6(0 - 1) (0 + 1)2 (0 - 3)2
= 6 × (- 1) × 1 × 9 = - 54 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, for x ∈ (-1, 1), function f is strictly decreasing.

(iii) For interval (1, 3)
f’(x) = 6(x - 1) (x + 1)2 (x - 3)2 > 0
For x = 2
f’(x) = 6(2 - 1) (2 + 1)2 (2 - 3)2
= 6 × 1 × 9 × 1 = 54 > 0
Similarly, by taking another points we can show that f’(x) > 0.
Thus, for x ∈ (1, 3), function f is strictly decreasing.

(iv) For interval (3, ∞)
f’(x) = 6(x - 1) (x + 1)2 (x - 3)2 > 0
For x = 4
f’(x) = 6(4 - 1) (4 + 1)2 (4 - 3)2
= 6 × 3 × 25 × 1
= 450 > 0
Similarly, by taking another points we can show that
f’(x) > 0.
Thus, for x ∈ (3, ∞), function f is strictly increasing.

Question 7.
Show that y = log(1 + x) - 2. $\frac{2x}{2+x}$, x > - 1 is an increasing function of x throughout its domain.
Answer:
Let y = f(x)

Thus, function is strictly increasing in its domain.
Hence Proved.

Question 8.
Find the values of x for which y = [x(x - 2)]2 is an increasing function.
Answer:
Let y = f(x)
= y = f(x) = [x(x - 2)]2
y = f(x) = (x2 - 2x)2
y = f(x) = x4 - 4x3 + 4x2
= $\frac{dy}{dx}$ = f’(x) = 4x3 - 12x2 + 8x
f’(x) = 4x(x2 - 3x + 2)
f’(x) = 0
4x(x2 - 3x + 2) = 0
4x(x - 2) (x - 1) = 0
x = 0 or x = 2 or x = 1
Point x = 0, x = 1 and x = 2 divide real number line into four disjoints intervals namely (- ∞, 0), (0, 1), (1, 2) and (2, ∞).

(i) For interval (- ∞, 0)
f’(x) = 4x3 - 12x2 + 8x
= 4x(x - 2) (x - 1) < 0
For x = - 1
f’(x) = 4(- 1)3 - 12(- 1)2 + 8(- 1)
= - 4 - 12 - 8 = - 24 < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, function is strictly decreasing for x ∈ (- ∞, 0).

(ii) For interval (0, 1)
f’(x) = 4x(x - 2) (x - 1) > 0
Fo x = $\frac{1}{2}$
f(x) = 4 × $\frac{1}{2}(\frac{1}{2}-2)(\frac{1}{2}-1)$
= 2$(-\frac{3}{2})(-\frac{1}{2})=\frac{3}{2}$ > 0
Similarly, by taking another points we can show that f’(x) >0.
Thus, function is strictly increasing for x ∈ (0, 1).

(iii) For interval (1, 2)
f’(x) = 4x(x - 1) (x - 2) < 0
For x = $\frac{3}{2}$
f’(x) = 4 $\times \frac{3}{2}(\frac{3}{2}-1)(\frac{3}{2}-2)$
= $6\left(\frac{1}{2}\right)(-\frac{1}{2})=-\frac{3}{2}$ < 0
Similarly, by taking another points we can show that f’(x) < 0.
Thus, function is strictly decreasing for x ∈ (1, 2).

(iv) For interval (2, ∞)
f’(x) = 4x(x - 1) (x - 2) > 0
For x = 3
f’(x) = 4 × 3(3 - 1) (3 - 2)
= 4 × 3 × 2 × 1 = 24 > 0
Similarly, by taking another points we can show that f’(x) > 0.
Thus, function is strictly increasing for x ∈ (2, ∞).
Hence, function is increasing in x ∈ (0, 1) ∪ (2, ∞).

Question 9.
Prove that y = $\frac{4\sin \theta }{(2+\cos \theta )}$ - θ is an increasing function of θ in $(0,\frac{\pi }{2})$.
Answer:
Let y = f(θ)

In interval $[0,\frac{\pi }{2}]$, cos θ > 0 and 4 - cos θ > 0, since - 1 ≤ cos θ ≤ 1 and (2 + cos θ)2 > 0.
∴ f’(θ) > 0
Hence, in interval [0, π/2], function f is strictly increasing.
Hence Proved.

Question 10.
Prove that the logarithmic function is increasing on (0, ∞).
Answer:
Let f(x) = log x, x > 0
⇒ f’(x) = $\frac{1}{x}$ > 0, for x > 0
∴ f’(x) > 0
Thus, logarithmic function is strictly increasing in (0, ∞).
Hence Proved.

Question 11.
Prove that the function f given by
f(x) = x2 - x + 1
is neither strictly increasing nor decreasing on (- 1, 1).
Answer:
Given, f(x) = x2 - x + 1
⇒ f’(x) = 2x - 1
f’(x) = 0 ⇒ 2x - 10
⇒ 2x = 1 ⇒ x = 1/2
Point x = $\frac{1}{2}$ divides line into two disjoints intervals namely $(-1,\frac{1}{2})$ and $(\frac{1}{2},1)$.

(i) For interval $(-1,\frac{1}{2})$
f’(x) = 2x - 1 < 0
For x = 0
f’(x) = 2 × 0 - 1 = - 1 < 0
Similarly, we can prove for other points f’(x) < 0. Thus,, for x ∈ $(-1;\frac{1}{2})$ function is strictly decreasing. (ii) For interval $(\frac{1}{2},1)$ f’(x) = 2x - 1 > 0
For x = $\frac{3}{4}$
f'(x) = 2 × $\frac{3}{4}$ - 1 = $\frac{3}{2}$ - 1 = $\frac{1}{2}$ > 0
Similarly, we can prove for other points f’(x) > 0.
Thus, function is strictly increasing for x ∈ $(\frac{1}{2},1)$.
Hence, function is decreasing in x ∈ $(-1,\frac{1}{2})$ and increasing in $(\frac{1}{2},1)$.
Hence, function is neither increasing nor decreasing in interval (- 1, 1).

Question 12.
Which of the following functions are decreasing in $(0,\frac{\pi }{2})$?
(A) cos x
Answer:
Let f(x) = cos x
f’(x) = - sin x
In interval $(0,\frac{\pi }{2})$, sin x > 0 ⇒ - sin x < 0
⇒ f’(x) < 0 Thus, function f(x) = cos x, is strictly decreasing in $(0,\frac{\pi }{2})$.

(B) cos 2x
Answer:
Let f(x) = cos 2x
⇒ f’(x) = - 2 sin 2x
In interval $(0,\frac{\pi }{2})$, sin 2x > 0 (0 < 2x < π)
⇒ - sin 2x < 0 ⇒ f'(x) < 0
Thus, in interval $(0,\frac{\pi }{2})$ cos 2x is strictly decreasing.

(C) cos 3x
Answer:
Let f(x) = cos 3x
⇒ f’(x) = - 3 sin 3x
When x ∈ $(0,\frac{\pi }{2})$
⇒ 0 < x < $\frac{\pi }{2}$
⇒ 0 < 3x < $\frac{\pi }{2}$
⇒ sin 3x may be + ve or - ve.
⇒ f’(x) = - 3 sin 3x is +ve and -ve.
Thus, in interval $(0,\frac{\pi }{2})$ function f is neither increasing nor decreasing.

(D) tan x
Answer:
Let f(x) = tan x
⇒ f’(x) = sec2x
In interval $(0,\frac{\pi }{2})$, sec x > 0
⇒ sec2 x > 0 ⇒ f’ (x) > 0
Thus, in interval $(0,\frac{\pi }{2})$, tan x is strictly increasing.

Question 13.
On 1rhich of the following intervals is the function f given by f(x) = x100 + sin x - 1 decreasing?
(A) (0, 1)
(B) $(\frac{\pi }{2},\pi )$
(C) $(0,\frac{\pi }{2})$
(D) none of these
Answer:
Given, f(x) = x100 + sin x - 1
f’(x) = 100x99 + cos x

(A) For interval (0, 1), 0 < x < 1
⇒ 0 < 100x99 < 100 and cos x > 0
∴ 100x99 + cos x > 0 ⇒ f’(x) > 0
∴ Function f(x) = x100 + sin x - 1 is increasing in interval (0, 1).

(B) For interval $(\frac{\pi }{2},\pi )$
x ∈ $(\frac{\pi }{2},\pi )$
⇒ x ∈ $(\frac{\pi }{2},\pi )$
⇒ x99 > 1
⇒ 100x99 > 100
∴ $(\frac{\pi }{2},\pi )$
∴ - 1 < cos x < 0 ⇒ 0 > cos x > - 1
∴ From equation (1) and (2)
100x99 + cos x > 100 - 1 = 99
100x99 + cos x > 0
⇒ f’(x) >0 (∴ f’(x) = 100x99 + cos x)
∴ In $(0,\frac{\pi }{2})$, f(x) is increasing.

(C) For interval $(0,\frac{\pi }{2})$
f’(x) = 100x99 + cos x > 0
Since cos x > 0 and 100x99 > 0
⇒ f’(x) > 0
∴ In interval $(0,\frac{\pi }{2})$ function j is increasing.
We see that function f is increasing for all intervals.
Hence, (D) is correct.

Question 14.
For what values of a the function f given by f(x) = x2 + ax + 1 is increasing on (1, 2)?
Answer:
Given, f(x) = x2 + ax + 1
⇒ f’(x) = 2x + a
x ∈ (1,2)
⇒ 1 < x < 2 ⇒ 2 < 2x < 4
⇒ 2 + a < 2x + a < 4 + a ⇒ 2 + a > 0
∴ a > - 2.
Thus, least value of a is - 2
For a = -2
f’(x) = 2x - 2 = 2(x - 1) > 0 [∴ 1 < x < 2]

Question 15.
Let be any interval disjoint from (-1, 1). Prove that the function f given by f(x) = x + $\frac{1}{x}$ is increasing on I.
Answer:
Given, f(x) = x + $\frac{1}{x}$
⇒ f(x) = 1 - $\frac{1}{x^2}$ = $\frac{x^2-1}{x^2}$
Given, I is such interval which is disjoint from (- 1, 1)
x < - 1 and x > 1
f’(x) > 0
If $\frac{x^2-1}{x^2}$ > 0 ⇒ x2 > 1
⇒ x < - 1 and x > 1
∴ In this interval f’(x) > 0.
Thus, function f is strictly increasing where x < -1, x > 1.
Hence, f(x), is strictly increasing in I.
Hence Proved.

Question 16.
Prove that the function f given by f(x) = log sin x, increasing on $(0,\frac{\pi }{2})$ and decreasing on $(\frac{\pi }{2},\pi )$.
Answer:
Given, f(x) = log sin x

Question 17.
Prove that the function f given by f(x) = log | cos x | is decreasing on $(0,\frac{\pi }{2})$ and increasing on $(\frac{3\pi }{2},2\pi )$.
Answer:
Given, f(x) = log cos x

Question 18.
Prove that the function given by f(x) = x3 - 3x2 + 3x -100 is increasing in R.
Answer:
f(x) = x3 - 3x2 + 3x - 100
f’(x) = 3x2 - 6x + 3
f’(x) = 3(x2 - 2x + 1)
f’(x) = 3(x - 1)2 > 0
f’(x) > 0 {∵ (x - 1)2 > 0 ∀ x ∈ R)
Hence, in function, R is strictly increasing.
Hence Proved.

Question 19.
The interval in which y = x2e is increasing is:
(A) (- ∞, ∞)
(B) (- 2, 0)
(C) (2, ∞)
(D) (0, 2)
Answer:
Let y = f(x) = x2e-x
⇒ f’(x) = $\frac{dy}{dx}$ = 2xe-x + x2 (- 1)e-x = 2xe- x - x2e-x
⇒ f’(x) = e-x.x (2 - x) = - xe-x (x - 2)
If function f is increasing, then
f’(x) > 0 ⇒ - x e-x (x - 2) > 0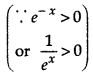

⇒ - x(x - 2) > 0
⇒ x(x - 2) < 0 ⇒ x ∈ (0, 2) ⇒ f’(x) > 0
∴ Function f is increasing in interval (0, 2).
Thus, (D) is correct.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !