RBSE Class 12 Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.6
Question 1.
x = 2at2, y = at4
Answer:
Given x = 2at2, y = at4
Differentiating both sides w.r.t t
Question 2.
x = a cos θ, y = b cos θ
Answer:
Given, x = a cos θ, y = b cos θ
Differentiating both sides w.r.t θ
Question 3.
x = sin t, y = cos 2t
Answer:
Given x = sin t and y = cos 2t
Differentiating both sides w.r.t t
Question 4.
x = 4t and y =
Answer:
Given, x = 4t and y =
Differentiating both sides w.r.t t
Question 5.
x = cos θ - cos 2θ, y = sin θ - sin 2θ
Answer:
Given, x = cos θ - cos 2θ
and y = sin θ - sin 2θ
Differentiating both sides w.r.t. θ
Question 6.
x = a(θ - sin θ), y = a(1 + cos θ)
Answer:
Given x = a(θ - sin θ)
and y = y = a(1 + cos θ)
Differentiating both sides w.r.t. θ
Question 8.
x = a(cos t + log tan t/2), y = a sin t
Answer:
x = a(cos t + log tan t/2), y = a sin t
Differentiating both sides of t
x = a(cos t + log tan t/2)
Question 9.
x = a sec θ, y = b tan θ
Answer:
Given, x = a sec θ, y = b tan θ
Differentiating both sides w.r.t. θ
Question 10.
x = a(cos θ + θ sin θ)
y = a(sin θ - θ cos θ)
Answer:
Given, x = a(cos θ + θ sin θ)
and y a(sin θ - θ cos θ)
Differentiating both functions w.r.t. θ
Question 11.
If x = and y = , then show that .
Answer:





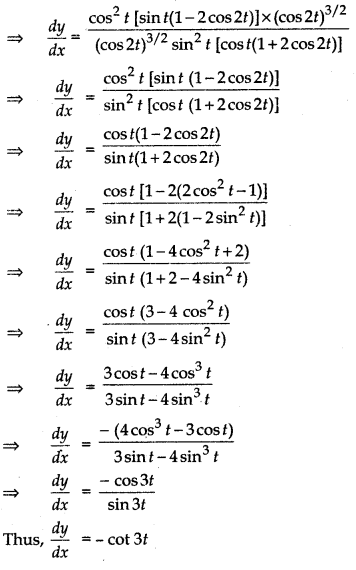

Either way the teacher or student will get the solution to the problem within 24 hours.