Chapter 6 Application of Derivatives Miscellaneous Exercise

Chapter 6 Application of Derivatives Miscellaneous Exercise

Question 1.

Using differentials, find the approximate value of each of the following:
(a) ${\left(\frac{17}{81}\right)}^{1/4}$
Answer:

(b) (33)-1/5
Answer:

Question 2.
Show that the function given by f (x) = $\frac{\log x}{x}$ has maximum at x = e.
Answer:

Question 3.
The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base?
Answer:
Let ∆ABC is an isosceles triangle.
In which AB = AC = x, BC = b (given)

Let M is the mid-point of base BC.

Question 4.
Find the equation of the normal to the curve x2 = 4y which passes through the point (1, 2).
Answer:
Equation of curve is x2 = 4y
⇒ y = $\frac{x^2}{4}$ ⇒ $\frac{dy}{dx}=\frac{2x}{4}=\frac{x}{2}$
∴ Slope of tangent at point (1, 2) = $\frac{1}{2}$ = m(say)
∴ Slope of normal at point (1, 2) is
= -$\frac{1}{m}=-\frac{1}{1/2}$ = - 2
∴ At point (1, 2) equation of normal is
y - 2 = (- 2) (x - 1)
⇒ y - 2 = - 2x + 2
⇒ 2x + y - 4 = 0
Thus, 2x + y - 4 = 0 is the required equation of the normal.

Question 5.
Show that the normal at any point θ to the curve x = a cos θ + aθ sin θ, y = a sin θ - a θ cos θ is at a constant distance from the origin.
Answer:
x = a cos θ + aθ sin θ and y = a sin θ - a θ cos θ
Differentiating x and y w. r. t. θ

∴ Equation of normal
y - (a sin θ - aθ cos θ) = - cot θ(x -(a cos θ + aθ sin θ)
Multiplying both sides by sin θ
y sin θ - a sin2θ + aθ cos θ sin θ
= sin θ × $(-\frac{\cos \theta }{\sin \theta })$ × [(x - (a cos θ + a θ sin θ)]
= y sin θ - a sin2θ + a θ cos θ sin θ
= - x cos θ + a cos2θ + a θ cos θ sin θ
= x cos θ + y sin θ = a sin2θ + a cos2θ
= x cos θ + y sin θ = a(sin2θ + cos2θ)
= x cos θ + y sin θ = a
Distance of normal from origin
$\left(\frac{0\times \cos \theta +0\times \sin \theta -a}{\sqrt{{\cos }^2\theta +{\sin }^2\theta }}\right)$ = |- a| (constant no.)
|- a| = a constant number (distance cannot be negative)
Thus, normal at curve is at a constant distance from origin.
Hence Proved.

Question 6.
Find the intervals in which the function f given by
f(x) = $\frac{4\sin x-2x-x\cos x}{2+\cos x}$, 0 ≤ x ≤ 2π
is (i) increasing, (ii) decreasing.
Answer:

Question 7.
Find the integrals in which the function f is given by:
f(x) = x3 + $\frac{1}{x^3}$, x ≠ 0
(i) increasing,
(ii) decreasing
Answer:
We have, f(x) = x3 + $\frac{1}{x^3}$
Differentiating w. r. t. x
f(x) = 3x2 - $\frac{3}{x^4}$
For increasing! decreasing f (x) = 0
⇒ 3x2 - $\frac{3}{x^4}$ = 0 ⇒ x2 = $\frac{1}{x^4}$
⇒ x6 = 1 ⇒ (x2)3 = 1 ⇒ x2 = 1
⇒ x = ±1 ∴ x = - 1, x = 1

(i) For interval (- ∞, - 1)

Similarly, we can show for other points.
∴ For x ∈ (- ∞, - 1) function is increasing.

(ii) For (- 1, 0)

Similarly, we can show for other points.
∴ In (- 1, 0) function is decreasing.

(iii) For (0, 1)

Similarly, we can show for other points.
∴ In (0, 1) function is decreasing.

(iv) For (1, ∞)

Thus, in (1, ∞) function is increasing.

Question 8.
Find the maximum area of an isosceles triangle inscribed in the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}$ = 1 with its vertex at one end of the major axis.
Answer:
Let P(a cos θ, b sin θ) be any point on ellipse and APQ is an isosceles triangle whose one vertex is one end of major axis.
Side PQ of ∆APQ cuts major axis at point M as shown in the following figure.

Area of ∆APQ A = $\frac{1}{2}$ PQ × AM
A = $\frac{1}{2}$ (2b sin θ) (a - a cos θ)
(∵ PQ = 2PM = 2b sin θ)
and AM = OA - OM = a - a cos θ)
A = $\frac{1}{2}$ ab × 2 sin θ(1 - cos θ)
A = ab(sin θ - sin θ cos θ) = ab (sin θ - $\frac{1}{2}$sin 2θ)
(∵ sin θ cos θ = $\frac{1}{2}$sin 2θ)
Differentiating w.r.t θ
$\frac{dA}{d\theta }$ = ab (cos θ - $\frac{1}{2}$ × 2 cos 2θ)
= ab (cos θ - cos 2θ) ....... (1)
A will be maximum, when $\frac{dA}{d\theta }$ = 0
⇒ ab(cos θ - cos 2θ) = 0 ⇒ cos θ - cos 2θ = 0
⇒ cos 2θ = cos θ ⇒ 2θ = 2π - θ
⇒ 3θ = 2π ⇒ θ = $\frac{2\pi }{3}$
Again, differentiating equation (1) w.r.t. θ

Question 9.
A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank costs ₹ 70 per square metres for the base and ₹ 45 per square metre for sides, what is the cost of least expensive tank?
Answer:
Let length and breadth of rectangular tank are x metres and y metres.

Depth of tank = 2m
Volume of tank = 2 × x × y = 8 (given)
⇒ xy = 4
Area of base = xy
Cost for the base = ₹ 70 per m2
∴ Total expanses for base = ₹ 70xy
Area of four walls = 2(x + y) × 2 = 4(x + y) m2
Rate of expenses on walls = ₹ 45 per m2
Total cost on walls = ₹ [45 × 4 (x + y)]
= ₹ 180 (x + y)
Then total expenses on walls and base
S = ₹ [70 xy + 180(x + y)] ......... (2)
From equation (1), putting y = $\frac{4}{x}$ in equation (2)


Thus, at x = 2 cost is minimum.
At x = 2, minimum cost S = 280 + 180 × 2 + $\frac{720}{2}$
= 280 + 360 + 360 = 1000
Thus, cost of least expensive S = ₹ 1,000

Question 10.
The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.
Answer:
Let x be the side of square and r be radius of circle.
Perimeter of square = 4x
Perimeter of circle (circumference) = 2πr
Sum of two perimeters = 4x + 2πr = k ..... (1)
Area of circle A1 = πr2
Area of square A2 = x2
∴ Sum of areas A = πr2 + x2 ............ (2)

Thus, side of square are twice the radius of circle whereas sum of both areas are minimum.
Hence Proved.

Question 11.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the windows is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
Answer:
Let ABCDPA is a window in which APD is semicircular. Centre of semi-circle is O.
∴ AD = 2r, AB = CD = x
Then, APD = $\frac{1}{2}$ × 2πr = πr

∴ Perimeter of window = 2x + 2r + πr
= 10 m
⇒ 10 = 2x + r(π + 2)
And area of window A = 2rx + $\frac{1}{2}$ πr2
From equation (1), 2x = 10 - (π + 2)r

Question 12.
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is ${(a^{\frac{2}{3}}+b^{\frac{2}{3}})}^{3/2}$
Answer:
Let ∆ABC is a right-angled triangle in which ∠B = 90°, and Pbe any point on hypotenure AC which is a distance from side AB and distance b from side BC.
Side PM is perpendicular to side AB and PN is perpendicular to side BC.
Again, let ∠ACB = θ = ∠APM.

∴ AP = a sec θ
PC = b cosec θ
Let length of hypotenuse is I, then
l = AP + PC
⇒ l = a sec θ + b cosec θ
Differentiating w. r. t. θ
$\frac{dl}{d\theta }$ = a sec θ tan θ - b cosec θ cot θ
For minimum l, $\frac{dl}{d\theta }$ = 0
a sec θ tan θ - b cosec θ cot θ = 0

Question 13.

Find the points at which the function f given by f(x) = (x - 2)4 (x + 1)3 has
(i) local maxima
(ii) local minima
(iii) point of inflexion
Answer:
Given, f(x) = (x - 2)4 (x + 1)3
Differentiating w. r. t. x
⇒ f'(x) = 4(x - 2)3 (x + 1)3 + 3(x - 2)4 (x + 1)2
⇒ f’(x) = (x - 2)3 (x + 1)2 [4(x + 1) + 3(x - 2)]
⇒ f'(x) = (x - 2)3 (x + 1)2 (4x + 4 + 3x - 6)
⇒ f'(x) = (x - 2)3 (x + 1)2 (7x - 2)
For local maxima/minima f (x) = 0
f'(x) = 0 = (x - 2)3 (x + 1)2 (7x - 2) = 0
⇒ (x - 2)3 = 0 or (x + 1)2 = 0 or 7x - 2 = 0
⇒ x = 2 or x = - 1 or x = $\frac{2}{7}$

(i) For x = - 1
x = - 1.1 taking (left side of - 1)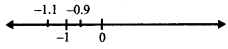

f' (- 1. 1) = (- 1.1 - 2)3 (- 1.1 + 1)2 [7(- 1.1) - 2]
⇒ f (x) = (- 3.1)3 (- 0.1)2 (- 9.7)
⇒ f (x) = (3.1)3 (- 0.1)2 (- 9.7)
⇒ f’ (1.1) = (3.1)3 (0.1)2 (9.7) > 0
Taking x = - 0.9 (right side of - 1)
f (- 0.9) = (- 0.9- 2)3 (- 0.9 + 1)2 {7(- 0.9) - 2}
f’ (- 0.9) = (- 2.9)3 (0.1)2 (- 6.3 - 2)
⇒ f (-0.9) = (- 2.9)3 (0.1)2 (- 8.3)
⇒ f (-0.9) = (2.9)3 (0.1) (8.3)
⇒ f (-0.9) = (2.9)3 (0.1) (8.3) > 0
Thus at x = -1 sign of function does not change.
∴ x = - 1 is point of inflection.

(ii) For x = $\frac{2}{7}$

∴ Sign of f'(x) changes from +ve to -ve
Thus, x = $\frac{2}{7}$ is local maximum point of function f.

(iii) For, x = 2 taking x = 1.9 (2 left side of),
[(1.9) = (1.9 - 2)2 (1.9 + 1)2 {7 × (1.9) - 2}
⇒ f’ (1.9) = (- 0.1)3 (2.9)3 (13.3 - 2)
⇒ f (1.9) = (- 0.1)3 (2.9)2 (11 3) < 0
Taking,x=2.1 (right sideof 2),
f (2.1) = (2.1 - 2)3 (2.1 + 1)2 (7 × 2.1 - 2)
⇒ f(2.1) = (0.1)3 (3.1)2 (14.7 - 2)
⇒ f(2.1) = (0.1)3 (3.1)2 (12.7) > 0
Thus, at x =2, sign of f (x) changes from -v to +ve.
∴ x = 2 is local minimum point of function.
(i) x = $\frac{2}{7}$ local maxima of function
(ii) x = 2 local minima of function
(iii) x = - 1 point of inflection of function

Question 14.

Find the absolute maximum and minimum values of the function f given by
f (x) = cos2 x + sin x, x ∈ [0, π]
Answer:
Given, f(x) = cos2 x + sin x
Differentiating w. r. t. x
f’(x) = 2 cos x(- sin x) + cos x
f’(x) = - 2 sin x cos x + cos x
f(x) = cos x(1 - 2 sin x)
For maxima/minima f’ (x) = 0
∴ f’(x) = 0 ⇒ cos x(1 - 2 sin x) = 0
cos x = 0 or 1 - 2 sin x = 0
x = π/2 or sin x = $\frac{1}{2}$ = sin $\left(\frac{\pi }{6}\right)$
x = π/2 or x = π/6
Now π/6, π/2 ∈ [0, π]
f(0) = cos2 0 + sin 0 = 1 + 0 = 1
f(π/6) = cos2(π/6) + sin(π/6)
= ${\left(\frac{\sqrt{3}}{2}\right)}^2+\frac{1}{2}=\frac{5}{4}$
f(π/2) = cos2(π/2) + sin π/2 = 0 + 1 = 1
f(π) = cos2π + sin π = (- 1)2 + 0 = 1
Thus, absolute maximum value = $\frac{5}{4}$
Absolute minimum value = 1

Question 15.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is $\frac{4r}{3}$.
Answer:
Let ABC is cone which is inscribed in a circle of radius r. O is the centre of circle.

Let radius of cone be R.
Height of cone (h) AM = AP - MP
AM = (2r - x) (∵ MP = x)
In right-angled ∆ 0MB,
OM2 + BM2 = OB2
(r - x)2 + R2 = r2
R2 = r2 - (r - x)2
R2 = r2 - (r2 - 2xr + x2)
R2 = r2 - r2 + 2rx - x2 = 2rx - x2

Question 16.
Let f be a function defined on [a, b] such that f(x) > 0 for all x ∈ (a, b). Then prove that f is an increasing function on [a, b].
Answer:
Let x1, x2 ∈ (a, b) such that for x1 < x2 f(x) is differentiable in interval (a, b) and [x1, x2] ∈ (a, b).
∴ f is continuous in internal [x1, x2] and differentiable in (x1, x2) then by mean value theorem.
∴ c ∈ (x1, x2) exists such that
f' (c) = $\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$ ......... (1)
Hence, for (a, b), f' (x) > 0
∵ f (c) > 0 [∵ c ∈ (x1, x2) c(a, b)]
⇒ c ∈ (a, b)
And f'(c) > 0 ⇒ $\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}$ > 0
⇒ f(x2) - f(x1) > 0 (∵ x2 - x1 > 0, when x1 < x2)
⇒ f(x2) > f(x1)
⇒ f(x1) < f(x2), If x1 < x2
Since x1, x2 ∈ (a, b) arbitrary points.
∴ x1 < x2 ⇒ f(x1) < f(x2) ∀ x1, x2 ∈ (a, b)
∴ f(x) is increasing function in interval [a, b].
Hence Proved.

Question 17.
Show that the height of the cylinder of maximum volume that can be inscribed In a sphere of radius R is $\frac{2R}{\sqrt{3}}$. Also, find the maximum volume.
Answer:
Let ABCD is a cylinder which be inscribed in a circle of radius R and volume of cylinder be V.
V = πr2h ........ (1)

Question 18.

Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi-vertical angle a is one-third that of the cone and the greatest volume of cylinder is $\frac{4}{27}$πh3 tan2 α.
Answer:
Let ABC is cone.
Height of cone = h
Semi-vertical angle = α
Cylinder PQRS is inscribed in cone ABC.
Let x be radius of cylinder.

Height of cylinder = MN = AN - AM
= h - x cot α
∵ In ∆ AMQ, cot α = $\frac{AM}{x}$
⇒ AM = x cot α
Volume of cylinder, V = πr2h(h - x cot α)
Differentiating w. r. t. x
$\frac{dV}{dx}$ = 2πx(h - x cot ) + πx2(- 1. cot α)
⇒ $\frac{dV}{dx}$ = 2πxh - 2πx2 cot α - πx2cot α
⇒ $\frac{dV}{dx}$ = 2πxh - 3πx2 cot α
Volume of cylinder will be maximum, if
$\frac{dV}{dx}$ = 0
⇒ 2πxh - 3πx2 cot α = α
⇒ πx(2h - 3x cot α) = 0
⇒ 2h - 3x cot α = 0 (∵ x ≠ 0)
⇒ x = $\frac{2h}{3\cot \alpha }$
Differentiating equ. (!) w.r.t.x.

∴ Height of cylinder = $\frac{1}{3}$h = $\frac{1}{3}$ (height of cone)
Thus, height of cylinder is one third height of cone.
Maximum volume of cylinder
= πx2 (h - x cot α)

Choose the correct answer in the Q. 19 to Q. 24

Question 19.
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of:
(A) 1 m/h
(B) 0.1 m/h
(C) 1.1 m/h
(D) 0.5 m/h
Answer:
Let H be height of cylinderical tank and r be radius.
Volume of tank V = πr2H
At, r = 10, V = π × 10 × 10 × H
∴ V = 100πH
Differentiating w. r. t. t

Question 20.
The slope of the tangent to the curve x = t2 + 3t - 8, y = 2t2 - 2t - 5 at the point (2, - 1) is:
(A) $\frac{22}{7}$
(B) $\frac{6}{7}$
(C) $\frac{7}{6}$
(D) -$\frac{6}{7}$
Answer:
Given, x = t2 + 3t - 8, y = 2t2 - 2t - 5
Differentiating x and y w.r.t t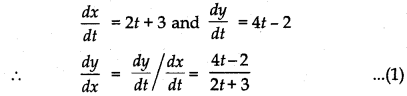

Putting x = 2 in x = t2 + 3t - 8
2 = t2 + 3t - 8
⇒ t2 + 3t - 8 - 2 = 0
⇒ t2 + 3t - 10 = 0
⇒ t2 + (5 - 2)t - 10 = 0
⇒ t2 + 5t - 2t - 10 = 0
⇒ t(t + 5)- 2 (t + 5) = 0
⇒ (t + 5) (t - 2) = 0
⇒ (t + 5) = 0 or (t - 2) = 0
⇒ t = - 5 or t = 2
Similarly, putting y = - 1 y = 2t2 - 2t - 5
- 1 = 2t2 - 2t - 5
⇒ 2t2 - 2t - 5 + 1 = 0
⇒ 2t2 - 2t - 4 = 0
⇒ t2 - t - 2 = 0
⇒ (t - 2) (t + 1) = 0
⇒ t - 2 = 0 or t + 1 = 0
⇒ t = 2 or t = - 1
t = 2 is common in both.
∴ At t = 2, $\frac{dy}{dx}=\frac{4\times 2-2}{2\times 2+3}=\frac{8-2}{4+3}=\frac{6}{7}$ [From equation (1)]
∴ Slope of tangent = $\frac{6}{7}$
Thus, (B) is correct. 

Question 21.

The line y = mx +1 is a tangent to the cuxve y2 = 4x if the value of m is:
(A) 1
(B) 2
(C) 3
(D) $\frac{1}{2}$
Answer:
Given, Curve y2 = 4x
Differentiating w. r. t. x

⇒ y1 = 0 or y1 = 2
But y1 ≠ 0
∴ y1 = 2
Putting y1 = 2 im equation my1 = 2
2m = 2 ⇒ m = 1
Thus, (A) is correct.

Question 22.
The normal at the point (1, 1) on the curve 2y + x2 = 3 is:
(A) x + y = 0
(B) x - y = 0
(C) x + y + 1 = 0
(D) x - y = 3
Answer:
Given, curve 2y + x2 = 3
Differentiating w. r. t. x

∴ Equation of normal is
y - 1 = 1 (x - 1)
Or y - 1 = x - 1 or x - y = 0
Thus, (B) is correct.

Question 23.

The normal to the curve 4y passing through (1, 2) is:
(A) x + y = 3
(B) x - y = 3
(C) x + y = 1
(D) x - y = 1
Answer:
Equation of curve is x2 = 4y
Differentiating w. r. t. x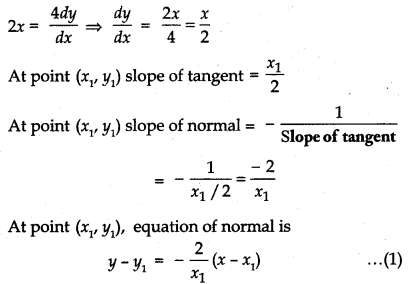

Given, that equation of normal passes through point (1, 2) then, from equation (1)
2 - y1 = - $\frac{2}{x_1}$(1 - x1)
⇒ 2x1 - x1y1 = - 2 + 2x1
⇒ x1y1 = 2 ⇒ y1 = $\frac{2}{x_1}$ ...... (2)
Point (x1, y1) thus lies on curve x2 = 4y.
x12 = 4y1 ........ (3)
From equation (2), putting value of y in equation (1)
x12 = 4 $\frac{2}{x_1}$ ⇒ x13 = 8 ⇒ x1 = 2
Putting value of x1 in equation (3)
(2)2 = 4y1 ⇒ 4 = 4y1 ⇒ y1 = 1
Putting x1 = 2 and y1 = 1 in equation (1)
y - 1 = $\frac{-2}{2}$ (x - 2)
⇒ y - 1 = - x + 2 ⇒ x + y = 3
So, the equation of normal is x + y = 3
Thus, (A) is correct.

Question 24.
The points on the curve 9y2 = x3, where the normal to the curve makes equal intercepts with the axes are:
(A) $(4,\pm \frac{8}{3})$
(B) $(4,-\frac{8}{3})$
(C) $(4,\pm \frac{3}{8})$
(D) $(\pm 4,\frac{3}{8})$
Answer:
Given, curve 9y2 = x3
Differentiating w.r.t. x

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !