RBSE Class 12 Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.1
Question 1.
Prove that the function f(x) = 5x - 3 is continuous at x = 0, at x = - 3 and at x = 5.
Answer:
Given, function, f(x) = 5x - 3
(ii) For continuity at x = 3
Question 2.
Examine the continuity of the function
f(x) = 2x2 - 1 at x = 3
Answer:
Given function, f(x) = 2x2 - 1
Question 3.
Examine the following functions for continuity.
(a) f(x) = x - 5
Answer:
Given, f(x) = x - 5
Given function is polynomial function.
Polynomial function is continuous everywhere.
Thus, (x - 5) also continuous everywhere.
i.e., function f is continuous everywhere, where x ∈ R.
(b) f(x) = , x ≠ 5
Answer:
f(x) = , x ≠ 5
Function is not defined at x = 5 so domain of function is R - [5]. Now x - 5 is polynomial function which is continuous everywhere in domain R - [5] and 1 is a constant function which is continuous everywhere.
Let g(x) = 1 and h(x) = (x - 5), x ≠ 5
Then f(x) =
which is a rational function which is continuous. Thus, function f(x) is continuous every where in domain R - {5}.
Note: Function f(x) is not defined at x = 5. Thus, it is not continuous at x = 5.
(c) f(x) =
, x ≠ - 5
Answer:
Given, f(x) = , x ≠ - 5
Function f(x) is not defined at x = - 5 so it is not continuous at x = - 5.
and domain of f(x) is R - {- 5}.
Let c ∈ R-{- 5} and c ≠ - 5
For continuity at x = c
Thus, function is continuous everywhere in domain R - {- 5}.
(d) f(x) = |x - 5|
Answer:
where c < 5
∴ Function is continuous at c < 5.
Thus, function is continuous everywhere in R.
Question 4.
Prove that the function f(x) = xn is continuous at x = n, where n is a positive integer.
Answer:
Given function f(x) = xn is a polynomial function. Polynomial function is continuous everywhere in domain R. Thus function f(x) = xn is continuous where x ∈ R and x ∈ N is positive integer. Hence Proved.
Question 5.
Is the function f defined by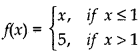
continuous at x = 0, at x = 1 and at x = 2?
Answer:
Given function,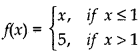
(ii) For continuity at x = 1
∴ (LHL) 1 ≠ 5 (RHL)
Thus, function is not continuous at x = 1.
(iii) For continuity at x = 2
Find all points of discontinuity of f, where f is defined by
Question 6.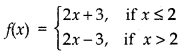
Answer:
Given function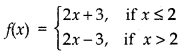
For continuity at x = 2
Thus, function is not continuous at x = 2 i.e., x = 2 is the point of discontinuity of f.
Question 7.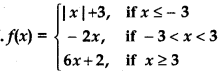
Answer:
(i) continuity of function at x = - 3
(ii) continuity of function at x = 3
So, function is not continuous at x = 3.
Thus, x = 3 is point of discontinuity of function.
Question 8.
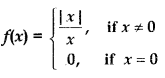
Answer:
For continuity at x = 0
∴ Function is not continuous at x = 0.
Thus, x = 0 is point of discontinuity of function.
Question 9.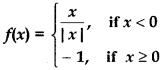
Answer:
For continuity of function at x = 0
So, function is continuous at x = 0.
Thus, there is no point of discontinuity of function.
Question 10.
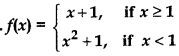
Answer:
For continuity of function at x = 1
Therefore, f is continuous at all points of x such that x > 1. Thus, the given function f has no point of discontinuity.
Question 11.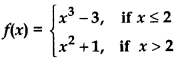
Answer:
For continuity of function at x = 2
value of function at x = 2
f(2) = 23 - 3 = 8 - 3 = 5
∴ f(x) = 5 = f(2), value of function at x = 2
Thus, given function is continuous at x = 2 and there is no point of discontinuity of function.
Question 12.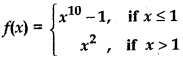
Answer:
Given function
For continuity of function at x = 1
Thus, function is not continuous at x = 1
∴ x = 1 is point of discontinuity of function.
Question 13.
Is the function defined by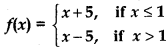
a continuous function?
Answer:
For continuity of function at x = 1
Discuss the continuity of the function f, when f is defined by:
Question 15.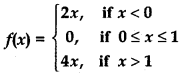
Answer:
(i) For continuity at x = 0
(ii) For continuity at x = 1
i.e., f(x) does not exists.
Thus, function is not continuous at x = 1, i.e., x = 1 is point of discontinuity of function.
Question 16.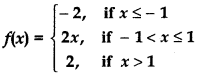
Answer:
(i) For continuity at x = - 1
(ii) For continuity at x = 1
Value of at f(x) x = 1 = f(1) = 2 × 1 = 2
∴ f(x) = 2 = f(1), value of f at x = 1
Thus, function is continuous at x = 1.
Question 17.
Find the relationship between a and b so that the function f defined by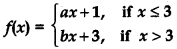
is continuous at x= 3.
Answer:
Function is continuous at x = 3
⇒ 3a = 3b + 3 - 1
⇒ 3a = 3b + 2
⇒ a = b +
If b = k an arbitrary real number,
then a = k +
Thus, a = k + and b = k
Question 18.
For what value of λ is the function defined by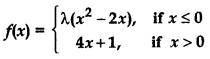
continuous at x = 0? What about continuity at x = 1?
Answer:
(i) For continuity at x = 0
Thus, function is not continuous at x = 0 for any value of λ.
(ii) For continuity at x = 1 
Value of f(x) at x = 1
f(1) = 4 × 1 + 1 = 4 + 1 = 5
∴ f(x) = 5 = f(1), value of f at x = 1
Thus, function is continuous at x = 1.
Question 19.
Show that the function defined by g(x) = x - [x] is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x.
Answer:
Given function, g(x) = x - [x]
(i) For continuity or discontinuity at x = 0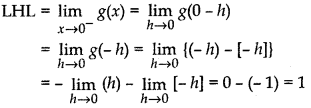
Since, -1 is the greatest integer before 0 as shown in real number line.
i.e., Left hand limit = 1 ≠ 0 = right hand limit
∴ g(x) does not exists.
∴ Function is not continuous at x = 0, i.e., discontinuous.
(ii) Let x = c ≠ 0, is any arbitrary real integer, then for continuity or discontinuity at x = c
Thus, function is not continuous at x = c, i.e., discontinuous.
Since, c is an arbitrary integer. Thus, g(x) is discontinuous at all integer.

Question 20.
Is the function defined by f(x) = x2 - sin x + 5 continuous at x = π ?
Answer:
Given function, f(x) = x2 - sin x + 5
For continuity at x = π
Question 21.
Discuss the continuity of the following functions:
(a) f(x) = sin x + cos x
Answer:
Given, f(x) = sin x + cos x
Let x = c be any arbitrary real number.
Then at x = c for continuity of function f(x) = sin x + cos x
Thus, function is continuous at x = c.
∵ c is an arbitrary real number.
∴ f(x) = sin x + cos x is continuous for all real numbers.
(b) f(x) = sin x - cos x
Answer:
Given, f(x) = sin x - cos x
Let x = c be any arbitrary real number.
Thus, for continuity of function f(x) = sin x - cos x at x = c
Thus, function is continuous at x = c.
∵ c is an arbitrary real number so function is continuous for all real numbers.
(c) f(x) = sin x.cos x
Answer:
Given, f(x) = sin x.cos x
Let x = c be any arbitrary real number, Now for continuity of function at x = c
∴ Function is continuous at x = C.
∵ x = c is an arbitrary real number. Thus, function is continuous for all real numbers.
Thus, function f(x) = sin x.cos x is continuous.
Question 22.
Discuss the continuity of the cosine, cosecant, secant and cotangent functions.
Answer:
(a) Continuity of cosine function
Let f(x) = cos x and x = c is an arbitrary real number.
For continuity of function at x = c
∴ Function is continuous at x = c.
∵ c is an arbitrary real number. Thus, function is continuous for all real numbers.
Therefore, cosine function is continuous.
(b) Continuity of cosecant function
Let f(x) = cosec x and x = c, where c ∈ R - {nπ}, n ∈ Z (n is integer). Since, cosec x is not defined for x = nπ.
For continuity of function at x = c [c ∈ R - {nπ}]
∴ Function is continuous at .i c, where c ∈ R - {nπ}.
∵ C ∈ R - {nπ} is an arbitrary real number. Thus, cosec function is continuous in domain R - {nπ}.
(c) Continuity of secant function
Let f(x) = sec’ x
and x = c ∈ R -
[since, at sec x is not defined and n ∈ Z]
For continuity at x = c
∴ Function is continuous at x c.
∵ c is an arbitrary real number. Thus, secant function is continuous for all real number, where
c ∈ R - {(2n + 1)}, n ∈ Z
(d) Continuity of cotangent function
Let f(x) = cot x and x = c is an arbitrary real number,
where C ∈ R - {nπ}, n ∈ Z since cot x, is not defined at x = nπ.
For continuity at x = c

∴ Function f(x) = cot x, c is continuous at C1 where c ∈ R - {nπ}, n ∈ Z.
∵ c is an arbitrary real number. Thus cotangent function is continuous for all values of R - {nπ}.
Question 23.
Find all points of discontinuity of f, where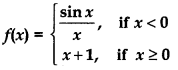
Answer:
∴ Function is continuous at x = 0.
Thus f(x) is continuous for all value of real number.
Therefore, there is no point of discontinuity of function.
Question 24.
Determine if f defined by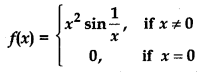
is a continuous function ?
Answer:
∴ Function is continuous at x = 0.
Thus f(x) is true for all real number.
Question 25.
Examine the continuity of f, where f is defined by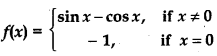
Answer:
Five continuity at x = 0
∴ Function is continuous at x = 0.
Thus, function f(x) is continuous for all real numbers.
Find the values of k so that the function f is continuous at the indicated point in Q. 26 to 29.
Question 29.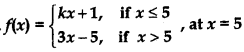
Answer:
⇒ 5k = 10 - 1 = 9 ⇒ k =
Thus, at k = function is continuous.
Question 30.
Find the values of a and b such that the function defined by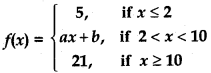
is a continuous function.
Answer:
Given function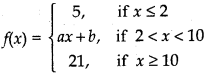
(i) For continuity of function at x = 2
(ii) For continuity of function at x = 10
∴ 10a + b = 21
Solving equation 2a + b = 5 and 10a + b = 21
a = 2, b = 1
Question 31.
Show that the function defined by f(x) = cos x2 is a continuous function.
Answer:
Given function, f(x) = cos x2
Let x = c ∈ R be any arbitrary real number, then
∴ Function is continuous at x = c.
Since, c is arbitrary real numbers.
∴ f is continuous for all real numbers.
Thus, function cos x2 is continuous.
Hence proved.
Question 32.
Show that the function defined by f(x) = |cos x| is a continuous function.
Answer:
Given function, f(x) = |cos x|
Let x = c ∈ R be any arbitrary real number, then
∴ Function is continuous at x = c
Since, c is an arbitrary real number. Therefore function is continuous for all real numbers.
Thus, function f(x) = |cos x| is continuous
Note: f(x) = |cos x|
If x < 0, f(x) = |cos (- x)| = |cos x| [Since, cos (- θ) = cos θ] and x > 0, f(x) = |cos x|
Hence Proved.
Question 33.
Examine that sin |x| is a continuous function.
Answer:
Given function, f(x) = sin |x|
Let x = c ∈ R be any arbitrary real number, then
∴ Function is continuous at x = c
Since, c is an arbitrary real number. so function is continuous for all real numbers.
Thus, function sin |x| is continuous.
Question 34.
Find all the points of discontinuity of f defined by f(x) = | x | - | x + 1 |.
Answer: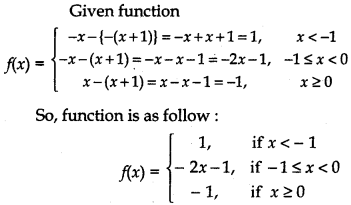
(ii) For or continuity at x = 0
∴ Function is continuous at x = 0.
Thus, there is no point of discontinuity of function.








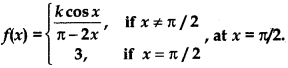


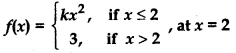

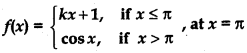



Either way the teacher or student will get the solution to the problem within 24 hours.