RBSE Class 12 Maths Solutions Chapter 4 Determinants Ex 4.5

RBSE Class 12 Maths Solutions Chapter 4 Determinants Ex 4.5

Question 1.

$\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$
Determinant of matrix A
|A| = $\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$ = (1 × 4) - (3 × 2) = 4 - 6 = - 2
If Aij is cofactor of aij in A, then
A11 = (- 1)1 + 1 |4| = 4
A12 = (- 1)1 + 2 |3| = - 3
A21 = (- 1)2 + 1 |2| = - 2
A22 = (- 1)2 + 2 |1| = 1
Matrix formed by the cofactors of |A| is
B (say) = $\left[\begin{array}{cc}4& -3\\ -2& 1\end{array}\right]$
Now, adj A = Transpose of B = $\left[\begin{array}{cc}4& -3\\ -2& 1\end{array}\right]$

Question 2.

$\left[\begin{array}{ccc}1& -1& 2\\ 2& 3& 5\\ -2& 0& 1\end{array}\right]$
Answer:

(3 × 1) - (0 × 5) + 1{2 × 1 - (- 2) × 5} + 2{2 × 0 - (- 2) × 3)
= 3 + 0 + 2 + 10 + 2(0 + 6)
= 3 + 2 + 10 + 12 = 27 ≠ 0
If Aij is cofactor of aij in A, then
A11 = (- 1)1 + 1 [(3 × 1) - (0 × 5)] = 3
A12 = (- 1)1 + 2 [(- 1) (2 + 10)0] = - 12
A13 = (- 1)1 + 3[2 × 0 - (- 2) × 3] = 0 + 6 = 6
A21 = (- 1)2 + 1 1 = [(- 1) (- 1)] = 1
A22 = (- 1)2 + 2 = [1 + 4] 5
A23 = (- 1)2 + 3 = [(- 1) (- 2)] = 2
A31 = (- 1)3 + 1 = [- 5 - 6] = - 11
A32 = (- 1)3 + 2 = [(- 1) (5 - 4)] = - 1
A33 = (- 1) 3 + 3 = [1 × 3 - 2(- 1)] = 3 + 2 = 5
Matrix formed by the cofactors of |A| is

Verify A(adj A) = (adj A) = |A| I in question 3 and 4:

Question 3.

$\left[\begin{array}{cc}2& 3\\ -4& -6\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{cc}2& 3\\ -4& -6\end{array}\right]$
Determinant of matrix A is
|A| = $\left|\begin{array}{cc}2& 3\\ -4& -6\end{array}\right|$
= 2 × (- 6) - (- 4) × 3 = - 12 + 12 = 0
If Aij is cofactor of aij in A then,
A11 = (- 1)1 + 1 (- 6) = - 6
A12 = (- 1)1 + 2 (- 4) = 4
A21 = (- 1)2 + 1 (3) = - 3
A22 = (- 1)2 + 2 (2) = 2
Matrix formed by the cofactors of |A| is

Question 4.

$\left[\begin{array}{ccc}1& -1& 2\\ 3& 0& -2\\ 1& 0& 3\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{ccc}1& -1& 2\\ 3& 0& -2\\ 1& 0& 3\end{array}\right]$
Determinant of A is
|A| = $\left|\begin{array}{ccc}1& -1& 2\\ 3& 0& -2\\ 1& 0& 3\end{array}\right|$
Expanding along C2, we get
|A| = {3 × 3 - 1 × (- 2)} + 0 + 0
∴ |A| = (9 + 2) = 11
A11 = (- 1)1 + 1 [(0 × 3 - 0 × (- 2)] = 3
A12 = (- 1)1 + 2 [(3 × 3 - 1) × (- 2 )] = (- 1) (9 + 2) = - 11
A13 = (- 1)1 + 3[(3 × 0 - 1 × 0)] = 0
A21 = (- 1)2 + 1 1 = [(- 1 × 3 - 0 × 2)] = (- 1) (- 3) = 3
A22 = (- 1)2 + 2 = [1 × 3 - 1 × 2] = 3 - 2 = 1
A23 = (- 1)2 + 3 = [1 × 0 - 1 × (- 1)] = - 1(0 + 1) = - 1
A31 = (- 1)3 + 1 = {- 1 × (- 2) - 0 × 2} = 2
A32 = (- 1)3 + 2 = {1 × (- 2) - 3 × 2} = (- 1) (- 2 - 6) = (- 1) (- 8) = 8
A33 = (- 1) 3 + 3 = [1 × 0 - 3 × (- 1)] = 8
Matrix formed by the cofactors of |A| is:

= |A| (∵ |A| = 11)
∴ (adj A)A = |A|I ........ (2)
From (1) and (2), we get
A(adj A) = (adj A)A = |A|I
Hence Proved.

Find the inverse of each of the matrices (if it exists) given in questions 5 to 11:

Question 5.
$\left[\begin{array}{cc}2& -2\\ 4& 3\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{cc}2& -2\\ 4& 3\end{array}\right]$
Determinant of A is:
|A| = $\left|\begin{array}{cc}2& -2\\ 4& 3\end{array}\right|$
= 2 × 3 - 4 × (- 2) = 6 + 8 = 14 ≠ 0
Then, matrix A is non-singular hence A-1 exists.
If Aij is cofactor of aij in A, then
A11 = (- 1)1 + 1 |3| = 3
A12 = (- 1)1 + 2 = - 4
A21 = (- 1)2 + 1 |- 2| = - (- 2) = 2
A22 = (- 1)2 + 2 |2| = 2
Matrix formed by the cofactor of A is

Question 6.
$\left[\begin{array}{cc}-1& 5\\ -3& 2\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{cc}-1& 5\\ -3& 2\end{array}\right]$
Determinant of matrix A is
|A| = $\left|\begin{array}{cc}-1& 5\\ -3& 2\end{array}\right|$
= - 1 × 2 - (- 3) × 5 = - 2 + 15 = 13 ≠ 0
Then matrix A is non-singular hence A-1 exists.
If Aij is cofactor of aij in A, then
A11 = (- 1)1 + 1 (2) = 2
A12 = (- 1)1 + 2 (- 3) = - (- 3) = 3
A21 = ( - 1)2 + 1 (5) = - 5
A22 = (- 1)2 + 2 (- 1) = - 1
Matrix formed by the cofactor of A is

Question 7.

$\left[\begin{array}{ccc}1& 2& 3\\ 0& 2& 4\\ 0& 0& 5\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{ccc}1& 2& 3\\ 0& 2& 4\\ 0& 0& 5\end{array}\right]$
Determinant of matrix A is
|A| = $\left[\begin{array}{ccc}1& 2& 3\\ 0& 2& 4\\ 0& 0& 5\end{array}\right]$
Expanding along C1
= 1(2 × 5 - 0 × 4) = 10 ≠ 0
Thus, matrix A is non-singuiar, i.e., A -1 exists.
If Aij is cofactor of in aij in A, then
A11 = (- 1)1 + 1[2 × 5 - 0 × 4] = 10
A12 = (- 1)1 + 2[(0 × 5 - 0 × 4)] = 0
A13 = (- 1)1 + 3[0 × 0 - 0 × 2)] = 0
A21 = (- 1)2 + 1[(- 1) (2 × 5 - 0 × 3)] = - 10
A22 = (- 1)2 + 2[(1 × 5 - 0 × 3)] = 5
A23 = (- 1)2 + 3[(- 1) (1 × 0 - 0 × 2)] = 0
A31 = (- 1)3 + 1[2 × 4 - 2 × 3 = 8 - 6] = 2
A32 = (- 1)3 + 2[(- 1) (1 × 4 - 0 × 3)] = - 4
A33 = (- 1)3 + 3[(1 × 2 - 0 × 2)] = 2
Matrix formed by the cofactors of |A| is

Question 8.
$\left[\begin{array}{ccc}1& 0& 0\\ 3& 3& 0\\ 5& 2& -1\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{ccc}1& 0& 0\\ 3& 3& 0\\ 5& 2& -1\end{array}\right]$
= 1{3 × (- 1) - 2 × 0} - 0 + 0 = - 3 ≠ 0
So, matrix A is non-singular, ie., A-1 exists.
If Aij is cofactor of aij in A, then
A11 = [3 × (- 1) - 2 × 0] = - 3
A12 = - [3 × (- 1) - 5 × 0] = - 1 (- 3) = 3
A13 = + [3 × 2 - 5 × 3] = 6 - 15 = - 9
A21 = - [0 × (- 1) - 2 × 0] = 0
A22 = +[1 × (- 1) - 5 × 0] = - 1
A23 = - [(1 × 2 - 5 × 0)] = - 2
A31 = +[0 × 0 - 3 × 0] = 0
A32 = - [(1 × 0 - 3 × 0)] = 0
A33 = +[1 × 3 - 3 × 0] = 3
Matrix formed by the cofactors of |A| is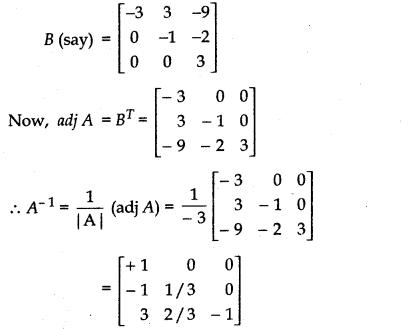

Question 9.

$\left[\begin{array}{ccc}2& 1& 3\\ 4& -1& 0\\ -7& 2& 1\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{ccc}2& 1& 3\\ 4& -1& 0\\ -7& 2& 1\end{array}\right]$
Determinant of matrix A is
|A| = $\left[\begin{array}{ccc}2& 1& 3\\ 4& -1& 0\\ -7& 2& 1\end{array}\right]$
= 2(- 1 × 1 - 2 × 0) - 1(4 × 1 - (- 7) × 0) + 3{4 × 2 - (- 7) × (- 1)}
= - 2 - 4 + 3(8 - 7) = - 2 - 4 + 3 = - 3 ≠ 0
So, matrix A is non-singular, i.e., A-1 exists.
If Aij is cofactor of aij in A, then
A11 = + [- (1 × 1) - (2 × 0)] = - 1
A12 = - [4 × 1 - (- 7) × 0] = - 4
A13 = +[4 × 2 - (- 7) × (- 1)] = 8 - 7 = 1
A21 = - [(1 × 1 - 2 × 3)] = (- 1) (1 - 6) = 5
A22 = +[2 × 1 - (- 7) × 3] = 2 + 21 = 23
A23 = - [2 × 2 - (- 7) × 1] = (- 1) (4 + 7) = - 11
A31 = + [1 × 0 - (- 1) × 3] = 3
A32 = - [(2 × 0 - 4 × 3)] = (- 1) (- 12) = 12
A33 = + [(2 × (- 1) - 4 × 1] = - 2 - 4 = - 6
Matrix formed by the cofactors of |A| is

Question 10.
$\left[\begin{array}{ccc}1& -1& 2\\ 0& 2& -3\\ 3& -2& 4\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{ccc}1& -1& 2\\ 0& 2& -3\\ 3& -2& 4\end{array}\right]$
Determinant of matrix A is
|A| = $\left[\begin{array}{ccc}1& -1& 2\\ 0& 2& -3\\ 3& -2& 4\end{array}\right]$
= 1{2 × 4 - (- 2) × (- 3)} + 1{0 × 4 - 3 × (- 3)} + 2{0 × (- 2) - 3 × 2}
= (8 - 6) + (0 + 9) + 2(- 6)
= 2 + 9 - 12 = - 1 ≠ 0
So, matrix A is non-singular, i.e., A-1 exists.
If Aij is cofactor of aij in A, then
A11 = (- 1)1 + 1[2 × 4 - (- 2) × (- 3)] = 8 - 6 = 2
A12 = (- 1)1 + 2 [0 × 4 - 3 × (- 3)] = - 1(+ 9) = - 9
A13 = (- 1)1 + 3 [0 × (- 2) - 3 × 2] = - 6
A21 = (- 1)2 + 1 [- 1 × 4 - (- 2) × 2] = (- 1) (- 4 + 4) = 0
A22 = (- 1)2 + 2 [1 × 4 - 3 × 2] = 4 - 6 = - 2
A23 = (- 1)2 + 3 [1 × (- 2) - 3 × (- 1)] = (- 1) (- 2 + 3) = - 1
A31 = (- 1)3 + 1 [(- 1) × (- 3) - 2 × 2] = 3 - 4 = - 1
A32 = (- 1)3 + 2 [1 × (- 3) - 0 × 2] = (- 1) (- 3) = 3
A33 = (- 1)3 + 3 [1 × 2 - 0 × (- 1)] = 2
Matrix formed by the cofactors of |A| is

Question 11.

$\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & \sin \alpha \\ 0& \sin \alpha & -\cos \alpha \end{array}\right]$
Answer:
Let A = $\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & \sin \alpha \\ 0& \sin \alpha & -\cos \alpha \end{array}\right]$
Determinant of matrix A is
|A| = $\left|\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & \sin \alpha \\ 0& \sin \alpha & -\cos \alpha \end{array}\right|$
= 1{cos α × (- cos α) - sin α (sin α)} - 0 + 0
= - cos2 α - sin2 a = - (cos2 α + sin2 α)
∴ | A | = - 1 ≠ 0
So, matrix A is non-singular, i.e., A-1 exists.
If Aij is cofactor of aij in A, then
A11 = +[cos α (- cos α - sin α (sin α)] = - cos2 α - sin2 α = - (cos2 α + sin2 α) = - 1
A12 = - {0 × (- cos α) - 0 × (sin α)} = 0
A13 = + [0 × sin α - 0 × cos α] = 0
A21 - [0 × (- cos α) - 0 × sin α] = 0
A22 = + [1 × (- cos α) - 0 × 0] = - cos α
A23 = - [(1 × sin α - 0 × 0)] = - sin α
A31 = + [0 × sin α - cos α × 0] = 0
A32 = - [(1 × sin α - 0 × 0)] = - sin α
A33 = + [1 × cos α - 0 × 0] = cos α
Matrix formed by the cofactors of |A| is

Question 12.
If A = $\left[\begin{array}{cc}3& 7\\ 2& 5\end{array}\right]$ and B = $\left[\begin{array}{cc}6& 8\\ 7& 9\end{array}\right]$, then verify that: (AB)-1 = B-1A-1
Answer:
Let A = $\left[\begin{array}{cc}3& 7\\ 2& 5\end{array}\right]$
Determinant of matrix A is
|A| = $\left|\begin{array}{cc}3& 7\\ 2& 5\end{array}\right|$
= 3 × 5 - 2 × 7 = 15 - 14 = 1 ≠ 0
So, matrix A is non-singular, i.e., A-1 exists.
If Aij is cofactor of aij in A, then
A11 = (- 1)1 + 1 (5) = 5
A12 = (- 1)1 + 2 (2) = - 2
A21 = (- 1)2 + 1 (7) = - 7
A22 = (- 1)2 + 2 (3) = 3
Matrix formed by the cofactors of |A| is

Determinant of matrix B is
|B| = $\left|\begin{array}{cc}6& 8\\ 7& 9\end{array}\right|$ = 6 × 9 - 7 × 8 = - 2 ≠ 0
∴ Matrix B is non-singular so B-1 exists.
If Bij is cofactor of bij in B, then
B11 = (- 1)1 + 1 (9) = 9
B12 = (- 1)1 + 2 (7) = - 7
B21 = (- 1)2 + 1 (8) = - 8
B22 = (- 1)2 + 2 (6) = 6
Matrix formed by the cofactor of |B| is

Question 13.

If A = $\left[\begin{array}{cc}3& 1\\ -1& 2\end{array}\right]$, show that A2 - 5A + 7I = 0. Hence, find A-1.
Answer:

∴ A2 - 5A + 7I = 0
⇒ A2 - 5A = - 7I
⇒ AA - 5A = - &I
Pre-multiplying both sides by A-1
(A-1A)A - 5A-1A = - 7A-1I
⇒ IA - 5I = - 7A-1 (∵ A-1A = I, A-1I = A-1)

Question 14.
For the matrix A = $\left[\begin{array}{cc}3& 2\\ 1& 1\end{array}\right],$ find the numbers a and b such that A2 + aA + bI = 0.
Answer:

⇒ 11 + 3a + b = 0 ........ (1)
8 + 2a = 0 .......... (2)
4 + a = 0 ............ (3)
3 + a + b = 0 .......... (4)
Now, from equation (3)
4 + a = 0
⇒ a = - 4
Putting a = - 4 in 3 + a + b = 0
3 - 4 + b = 0
⇒ - 1 + b = 0 ⇒ b = 1
Thus a = - 4, b = 1
By a = - 4, b = 1 solving 11 + 3a + b = 0 and 8 + 2a = 0.
11 + 3 × (- 4) + 1 = 11 - 12 + 1 = 0
And 8 + 2 × (- 4) = 8 - 8 = 0
Thus, a and b satisfies 11 + 3a + b = 0 and 8 + 2a = 0.

Question 15.

For the matrix A = $\left[\begin{array}{ccc}1& 1& 1\\ 1& 2& -3\\ 2& -1& 3\end{array}\right]$, show that A3 - 6A2 + 5A + 11I = 0. Hence, find A-1.
Answer:


Thus, A3 - 6A2 + 5A + 11I = 0
Multiplying equation A3 - 6A2 + 5A + 11I = 0 by A-1
(A-1A)A2 - 6(AA-1)A + 5(A-1A) + 11(A-1I) = A-1 = 0
⇒ IA2 - 6IA + 5I + 11A-1 = 0
[∵ A-1 A = I, A-1I = A-1, A-10 = 0]
⇒ A2 - 6A + 5I + 11A-1 = 0, (∵ IA = A)
⇒ 11A-1 = - A2 + 6A - 5I

Question 16.

If A = $\left[\begin{array}{ccc}2& -1& 1\\ -1& 2& -1\\ 1& -1& 2\end{array}\right]$, verify that A3 - 6A2 + 9A - 4I = 0 and hence find A-1.
Answer:

Question 17.

If A be a non-singular square matrix of order 3 × 3, then | adj A | is equal to:
(A) | A |
(B) | A |2
(C) | A |3
(D) 3| A |
Answer:
Given, A be a square matrix of order n × n, then
| adj A |=| A |n - 1
Here n = 3
∴ |adjA | = | A |3 - 1 = | A |2
Thus, option (B) is correct.

Question 18.
If A be an invertible matrix of order 2, then det (A-1) is equal to:
(A) det
(B) $\frac{1}{det\left(A\right)}$
(C) 1
(D) 0
Answer:
Since, A is invertible matrix so its determinant value will not be zero, i.e.,
|A| ≠ 0
∴ AA-1 = 1
⇒ |AA-1| = | I | = 1
⇒ |A| |A-1| = 1 (∵ |AB| = |A| |B|)
⇒ |A-1| = $\frac{1}{|A|}$
⇒ det(A-1) = $\frac{1}{det\left(A\right)}$
Thus, option (B) is correct.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !