RBSE Class 12 Maths Solutions Chapter 4 Determinants Miscellaneous Exercise

RBSE Class 12 Maths Solutions Chapter 4 Determinants Miscellaneous Exercise

Question 1.

Prove that the determinant x $\left|\begin{array}{ccc}x& \sin \theta & \cos \theta \\ -\sin \theta & -x& 1\\ \cos \theta & 1& x\end{array}\right|$ is independent of θ.
Answer:

= x(- x2 - 1) - sin θ (- x sin θ - cos θ) + cos θ (- sin θ + x cos θ)
= x(- x2 - 1) + x sin2 θ + sin θ cos θ - cos θ sin θ + x cos2 θ
= - x3 - x + x(sin2 θ + cos2 θ)
= - x3 - x + x × 1 = - x3
Clearly, ∆ is independent of θ.
Hence Proved.

Question 2.

Without expanding the determinant, prove that
$\left|\begin{array}{ccc}a& a^2& bc\\ b& b^2& ca\\ c& c^2& ab\end{array}\right|$=$\left|\begin{array}{ccc}1& a^2& a^3\\ 1& b^2& b^3\\ 1& c^2& c^3\end{array}\right|$
Answer:

Question 3.
Evaluate
$\left|\begin{array}{ccc}\cos \alpha \cos \beta & \cos \alpha \sin \beta & -\sin \alpha \\ -\sin \beta & \cos \beta & 0\\ \sin \alpha \cos \beta & \sin \alpha \sin \beta & \cos \alpha \end{array}\right|$
Answer:

Question 4.

If a, b and c are real numbers and
Δ = $\left|\begin{array}{ccc}b+c& c+a& a+b\\ c+a& a+b& b+c\\ a+b& b+c& c+a\end{array}\right|$ = 0
then show that either a + b + c = 0 and a = b = c.
Answer:
Given determinant is:

⇒ 2(a + b + c) {(b - c) × (c - b) - (c - a) (b - a)} = 0
⇒ 2(a + b + c) {- (b - c)2 - (cb - ca - ab + a2)} = 0
⇒ 2(a + b + c) {- b2 - c2 + 2bc - bc + ca + ab - a2} = 0
⇒ 2(a + b + c) × {- a2 - b2 - c2 + bc + ca + ab} = 0
⇒ - 2(a + b + c) × {a2 + b2 + c2 - ab - bc - ca] = 0
⇒ -(a + b + c) {2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca] = 0
⇒ - (a + b + c) {(a2 + b2 - 2ab + b2 + c2 - 2ab + c2 + a2 - 2ac} = 0
⇒ - (a + b + c) × {(a - b)2 + {b - c)2 + (c - a)2} = 0
⇒ a + b + c = 0
or (a - b)2 + (b - c)22 + (c - a)2 = 0
⇒ a - b = 0, b - c = 0, c - a = 0
⇒ a = b, b = c, c = a
⇒ a = b = c
Hence a + b + c = 0
or a = b = c
Hence Proved.

Question 5.

If a ≠ 0 then, solve
$\left|\begin{array}{ccc}x+a& x& x\\ x& x+a& x\\ x& x& x+a\end{array}\right|$ = 0
Answer:

Question 6.
Prove that
$\left|\begin{array}{ccc}{a}^2& bc& ac+c^2\\ a^2+ab& b^2& ac\\ ab& b^2+bc& c^2\end{array}\right|$ = 4a2b2c2
Answer:

= 2a2b2c {(a + c) (1 - 0) - 1(a + b -b - c)}
= 2a2b2c{a + c - a - b + b + c}
= 2a2b2c(2c)
= 4a2b2c2
Hence Proved.

Question 7.

If A-1 = $\left[\begin{array}{ccc}3& -1& 1\\ -15& 6& -5\\ 5& -2& 2\end{array}\right]$ and B = $\left[\begin{array}{ccc}1& 2& -2\\ -1& 3& 0\\ 0& -2& 1\end{array}\right]$ then find the value of (AB)-1.
Answer:
We have,

= 1(3 - 0) - 2(-1 - 0) - 2(2 - 0)
= 3 + 2 - 4 = 1
∴ |B| = 1 ≠ 0
Since, B is non-singular so B-1 exists.
If Bij is cofactor of bij in B, then
B11 = + [3 × 1 - (- 2) × 0] = 3
B12 = (- 1) (- 1) - 0 = 1
B13 = + [(- 1) × (- 2) - 0 × 3] = 2
B21 = (- 1) (2 - 4) = (- 1) (- 2) = 2
B22 = + [1 × 1 - 0 (- 2) = 1
B23 = (- 1) [1 × (- 2) - 0 × 2] = 2
B31 = + [2 × 0 - 3 × (- 2)] = 6
B32 = (- 1) [0 - (- 1) (- 2)] = 2
B33 = + [1 × 3 - (-1) × 2] = 3 + 2 = 5

Question 8.

Let A = $\left[\begin{array}{ccc}1& -2& 1\\ -2& 3& 1\\ 1& 1& 5\end{array}\right]$, then verify that
(i) (adj A)-1 = (adj) A-1
Answer:
Given, A = $\left[\begin{array}{ccc}1& -2& 1\\ -2& 3& 1\\ 1& 1& 5\end{array}\right]$
Determinant of matrix A,
|A| = $\left|\begin{array}{ccc}1& -2& 1\\ -2& 3& 1\\ 1& 1& 5\end{array}\right|$
= (15 - 1) + 2(- 10 - 1) + (- 2 - 3)
= 14 + 2(- 11) + (- 5)
= 14 - 22 - 5 = - 13
∴ | A | = - 13 ≠ 0
Since, matrix A is non-singular so A-1 exists.
If Aij is cofactor of aij in A, then
A11 = + [3 × 5 - 1 × 1] = 15 - 1 = 14
A12 = (- 1) [- 10 - 1] = 11
A13 = + [- 2 × 1 - 1 × 3] = - 2 - 3 = - 5
A21 = (- 1) [- 10 - 1] = (- 1) × (- 11) = 11
A22 = + [1 × 5 - 1 × 1] = 5 - 1 = 4
A23 = (- 1) [1 + 2] = (- 1) × 3 = - 3
A31 = + [- 2 × 1 - 3 × 1] = - 2 - 3 = - 5
A32 = (- 1) [1 + 2] = (- 1) (3) = - 3
A33 = + [1 × 3 - (- 2) × (- 2)] = 3 - 4 = - 1

= 14(- 4 - 9) - 11(- 11 - 15) - 5(- 33 + 20)
= 14(- 13) - 11(- 26) - 5 (-13)
= - 182 + 286 + 65 = 169
∴ |B| = 169 ≠ 0
Since, matrix B is non-singular so B-1 exists.
If Bij is cofactor of bij in B, then
B11 = + [4 × (-1) - (- 3) × (- 3)] = - 4 - 9 = -13
B12 = (- 1) (- 11 - 15)] = (- 1) (- 26) = 26
B13 = + [11 × (- 3) - (- 5) × 4] = - 33 + 20 = - 13
B21 = (- 1) [- 11 - 15)] = (- 1) (- 26) = 26
B22 = + [14 × (- 1) - (- 5) × (- 5)] = -14 - 25 = - 39
B23 = (- 1) (- 42 + 55) = (- 1) (13) = - 13
B31 = + [11 × (- 3) - 4 × (- 5)] = - 33 + 20 = - 13
B32 = (- 1) [- 42 + 55] = (- 1) (13) = - 13
B33 = + [14 × 4 - 11 × 11] = 56 - 121 = - 65

(ii) (A-1)-1 = A

Answer:

Question 9.
Evaluate: $\left|\begin{array}{ccc}x& y& x+y\\ y& x+y& x\\ x+y& x& y\end{array}\right|$
Answer:

= 2(x + y) {x × (- x) - (x - y) × (- y)}
= 2(x + y) {- x2 + xy - y2}
= - 2(x + y) (x2 - xy + y2)
= - 2(x3 + y3)

Question 10.

$\left|\begin{array}{ccc}1& x& y\\ 1& x+y& y\\ 1& x& x+y\end{array}\right|$
Answer:

Using properties of determinants in Question 11 to 15. Prove that

Question 11.
$\left|\begin{array}{ccc}\alpha & {\alpha }^2& \beta +\gamma \\ \beta & {\beta }^2& \gamma +\alpha \\ \gamma & {\gamma }^2& \alpha +\beta \end{array}\right|$ = (β - γ) (γ - α) (α - β) (α + β + γ)
Answer:

Applying R2 → R2 - R1 and R3 → R3 - R1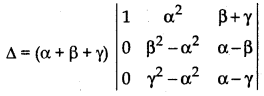

Taking common (β - α) and (γ - α) from R2 and R3 respectively

⇒ ∆ = (α + β + γ) (β - α) (γ - α) × {(β - α) (- 1) - (γ + α) (- 1)}
⇒ ∆ = (α + β + γ) (β - α) (γ - α) × (- β - α + γ + α)
⇒ ∆ = (α + β + γ) (β - α) (γ - α) (- β + γ)
⇒ ∆ = (α + β + γ) (α - β) (γ - α) (γ - β) [∵ (β - α) = - (α - β), (γ - β) = - (β - γ)]
⇒ ∆ = (α + β + γ) (α - β) (β - γ) (γ - α)
= R.H.S
Hence Proved.

Question 12.

$\left|\begin{array}{ccc}x& x^2& 1+p{x}^3\\ y& y^2& 1+p{y}^3\\ z& z^2& 1+p{z}^3\end{array}\right|$ = (1 + pxyz) (x - y) (y - z) (z - x), where p is any scalar.
Answer:

Now, in ∆1, applying R2 → R2 - R1 and R3 → R3 - R1
∆1 = $\left|\begin{array}{ccc}x& x^2& 1\\ y-x& y^2-x^2& 0\\ z-x& z^2-x^2& 0\end{array}\right|$
Taking factor (y - z) and (z - x) common from R2 and R3 respectively

⇒ ∆1 = (y - x) (z - x) {1(z + x) - 1 × (y + x)}
⇒ ∆1 = (y - x) (z - x) {z + x - y - x}
⇒ ∆1 = (y - x) (z - x) (z - y)
⇒ ∆1 = (x - y) (y - z) (z - x)
[∵ (y - x) = - (x - y) and (z - y) = - (y - z)]
∴ ∆1 = (x - y) (y - z) (z - x) ...... (2)
Now ∆2 = $\left|\begin{array}{ccc}x& x^2& p{x}^3\\ y& y^2& p{y}^3\\ z& z^2& p{z}^3\end{array}\right|$
Taking x, y, z common from R1, R2 and R3 respectively and p from C3

Again, taking common (y - x) and (z - x) from R2 and R3 respectively,
∆2 = pxyz(y - x) (z - x) $\left|\begin{array}{ccc}1& x& x^2\\ 0& 1& y+x\\ 0& 1& z+x\end{array}\right|$
Now, expanding ∆2 along C1
⇒ ∆2 = pxyz(y - x) (z - x) × $\{1\left|\begin{array}{cc}1& y+x\\ 1& z+x\end{array}\right|-0+0\}$
⇒ ∆2 = pxyz(y - x) (z - x) × {1 × (z + x) - 1 × (y + x)}
⇒ ∆2 = pxyz{y - x) (z - x) (z + x - y - x)
⇒ ∆2 = pxyz(y - x) (z - x) (z - y)
⇒ ∆2 = pxyz(x - y) (y - z) (z - x)
[∵ (y - x) = -(x - y) and (z - y) = - (y - z)]
∴ ∆2 = pxyz(x - y) (y - z) (z - x) ....... (3)
Now, substituting the values of ∆1 and ∆2 in equation (1), we get
∆ = (x - y) (y - z) (z - x) + pxyz(x - y) (y - z) (z - x)
⇒ ∆ = (x - y) (y - z) (z - x) (1 + pxyz)
∴ ∆ = (1 + pxyz) (x - y) (y - z) (z - x)
= R.H.S.
Hence Proved.

Question 13.

$\left|\begin{array}{ccc}3a& -a+b& -a+c\\ -b+a& 3b& -b+c\\ -c+a& -c+b& 3c\end{array}\right|$ = 3(a + b + c) (ab + bc + ca)
Answer:

⇒ ∆ = (a + b + c) {(a + 2b) (2c + a) - (- c + a) (- b + a)}
⇒ ∆ = (a + b + c) {2ca + a2 + 4bc + 2ba - (bc - ac- ab + a2)}
⇒ ∆ = (a + b + c) {(2ca + a2 + 4bc - bc + ac + ab - a2 + 2ab}
⇒ ∆ = (a + b + c) {3ab + 3bc + 3ca}
⇒ ∆ = (a + b + c) × 3 (ab + bc + ca)
⇒ ∆ = 3 (a + b + c) (ab + bc + ca)
∴ ∆ = 3 (a + b + c) (ab + bc + a)

Question 14.

$\left|\begin{array}{ccc}1& 1+p& 1+p+q\\ 2& 3+2p& 4+3p+2q\\ 3& 6+3p& 10+6p+3q\end{array}\right|$ = 1
Answer:

Question 15.

$\left|\begin{array}{ccc}\sin \alpha & \cos \alpha & \cos (\alpha +\delta )\\ \sin \beta & \cos \beta & \cos (\beta +\delta )\\ \sin \gamma & \cos \gamma & \cos (\gamma +\delta )\end{array}\right|$ = 0
Answer:

Thus, ∆ = 0 (all elements of C3 are zero)
Hence Proved.

Question 16.
Solve the following equations :
$\frac{2}{x}+\frac{3}{y}+\frac{10}{z}$ = 4
$\frac{4}{x}-\frac{6}{y}+\frac{5}{z}$ = 1
$\frac{6}{x}+\frac{9}{y}-\frac{20}{z}$ = 2
Answer:
Given system of equation is
$\frac{2}{x}+\frac{3}{y}+\frac{10}{z}$ = 4
$\frac{4}{x}-\frac{6}{y}+\frac{5}{z}$ = 1
$\frac{6}{x}+\frac{9}{y}-\frac{20}{z}$ = 2
Let u = $\frac{1}{x}$, v = $\frac{1}{y}$ and w = $\frac{1}{z}$ then
2u + 3v + 10 w = 4
4u - 6v + 5w = 1
6u + 9v - 20w = 2
Writing in matrix form
AX = B ....... (1)

⇒ |A| = 2 × 75 - 3 × (- 110) + 10 x× 72
⇒ |A| = 150 + 330 + 720 = 1200
∴ |A| = 1200 ≠ 0
Since, matrix A is non-singular so A-1 exists.
If Aij is cofactor of aij in A, then
A11 = + [- 6 × (- 20) - 9 × 5] = 120 - 45 = 75
A12 = (- 1) [- 80 - 30] = (- 1) (- 110) = 110
A13 = + [4 × 9 - 6 × (- 6)] = 36 + 36 = 72
A21 = (- 1) (- 60 - 90) = (- 1) (- 150) = 150
A22 = + [- 40 - 60] = - 100
A23 = (- 1) [18 - 18] = 0
A31 = + [3 × 5 - (- 6) × 10] = 15 + 60 = 75
A32 = (- 1) (10 - 40) = (-1) (- 30) = 30
A33 = + [2 × (- 6) - 4 × 3] = - 12 - 12 = - 24

Question 17.

If a,b,c are in A.P., then the determinant $\left|\begin{array}{ccc}x+2& x+3& x+2a\\ x+3& x+4& x+2b\\ x+4& x+5& x+2c\end{array}\right|$ is:
(A) 0
(B) 1
(C) x
(D) 2x
Answer:

All element of R2 are zero.
Thus, option (A) is correct.

Question 18.
If x, y, z are non-zero real numbers, then the inverse of matrix A = $\le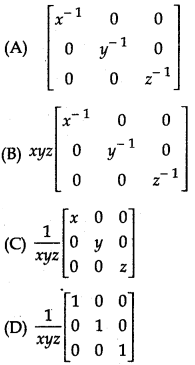ft[\begin{array}{ccc}x& 0& 0\\ 0& y& 0\\ 0& 0& z\end{array}\right]$ is:

Answer:
Let A = $\left[\begin{array}{ccc}x& 0& 0\\ 0& y& 0\\ 0& 0& z\end{array}\right]$
∴ Determinant of matrix A is
|A| = x$\left|\begin{array}{cc}y& 0\\ 0& z\end{array}\right|$ - 0 + 0
= x(yz - 0) = xyz
∴ |A| = xyz ≠ 0
If Aij is cofactor of aij in A, then
A11 = + [yz - 0] = yz
A12 = (- 1) (0 × z - 0 × 0) = 0
A13 = + [0 × 0 - 0 × y = 0]
A21 = (- 1) (0 × z - 0 × 0) = 0
A22 = + [xz - 0 × 0] = xz
A23 = (- 1) (x × 0 - 0 × 0) = 0
A31 = + [0 × 0 - 0 × y] = 0
A32 = (- 1) [x × 0 - 0 × 0] = 0
A33 = + [x × y - 0 × 0] = xy

Thus, option (A) is correct.

Question 19.

If A = $\left[\begin{array}{ccc}1& \sin \theta & 1\\ -\sin \theta & 1& \sin \theta \\ -1& -\sin \theta & 1\end{array}\right]$, where 0 ≤ θ ≤ 2π, then
(A) Det (A) = 0
(B) Det (A) ∈ (2, ∞)
(C) Det (A) ∈ (2, 4)
(D) Det (A) ∈ [2, 4]
Answer:

⇒ (1 + sin2θ) + (sin2θ - sin2θ) + (sin2θ + 1)
⇒ |A| = 1 + sin2θ + sin2θ + 1
⇒ |A| = 2(1 + sin2θ)
Now θ = 0, |A| = 2
θ = $\frac{\pi }{2}$,
|A| = 2(1 + 1) = 4
∴ det (A) ∈ [2, 4]
Thus, option (D) is correct.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !