RBSE Class 12 Maths Solutions Chapter 3 Matrices Ex 3.3

RBSE Class 12 Maths Solutions Chapter 3 Matrices Ex 3.3

Question 1.

Find the response of each of the following matrices:
(i) $\left[\begin{array}{c}5\\ \frac{1}{2}\\ -1\end{array}\right]$
Answer:
$\left[\begin{array}{ccc}5& \frac{1}{2}& -1\end{array}\right]$

(ii) $\left[\begin{array}{cc}1& -1\\ 2& 3\end{array}\right]$
Answer:
$\left[\begin{array}{cc}1& 2\\ -1& 3\end{array}\right]$

(iii) $\left[\begin{array}{ccc}-1& 5& 6\\ \sqrt{3}& 5& 6\\ 2& 3& -1\end{array}\right]$
Answer:
$\left[\begin{array}{ccc}-1& \sqrt{3}& 2\\ 5& 5& 3\\ 6& 6& -1\end{array}\right]$

Question 2.
If A = $\left[\begin{array}{ccc}-1& 2& 3\\ 5& 7& 9\\ -2& 1& 1\end{array}\right]$ and B = $\left[\begin{array}{ccc}-4& 1& -5\\ 1& 2& 0\\ 1& 3& 1\end{array}\right]$ then verify that
(i) (A + B)' = A' + B'
Answer:

(ii) (A - B)' = A' - B'
Answer:

Question 3.
If A' = $\left[\begin{array}{cc}3& 4\\ -1& 2\\ 0& 1\end{array}\right]$ and B = $\left[\begin{array}{ccc}-1& 2& 1\\ 1& 2& 3\end{array}\right]$ then verify that
(i) (A + B)' = A' + B'
Answer:

(ii) (A - B)' = A' - B'
Answer:

Question 4.
If A' = $\left[\begin{array}{cc}-2& 3\\ 1& 2\end{array}\right]$ and B = $\left[\begin{array}{cc}-1& 0\\ 1& 2\end{array}\right]$, then find (A + 2B).
Answer:

Question 5.
For the matrices A and B verify that (AB)' = B'A', where
(i) A = $\left[\begin{array}{c}1\\ -4\\ 3\end{array}\right]$
Answer:

(ii) A = $\left[\begin{array}{c}0\\ 1\\ 2\end{array}\right]$, B = [1 5 7]
Answer:

Question 6.
(i) If A = $\left[\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right]$, then verify that AA' = I.
Answer:

(ii) If A = $\left[\begin{array}{cc}\sin \alpha & \cos \alpha \\ -\cos \alpha & \sin \alpha \end{array}\right]$ , then verify that A'A = I.
Answer:

Question 7.
(i) Show that the matrix A = $\left[\begin{array}{ccc}1& -1& 5\\ -1& 2& 1\\ 5& 1& 3\end{array}\right]$ is a symmetric matrix.
Answer:

(ii) Prove that the matrix A = $\left[\begin{array}{ccc}0& 1& -1\\ -1& 0& 1\\ 1& -1& 0\end{array}\right]$ is a skew-symmetric matrix.
Answer:

Question 8.
For matrix A = $\left[\begin{array}{cc}1& 5\\ 6& 7\end{array}\right]$, verify that
(i) (A + A') is a symmetric matrix
Answer:

= A + A'
∴ (A + A')' = A + A'
Thus, A + A' is a symmetric matrix.

(ii) (A - A') is a skew-symmetric matrix
Answer:

= - (A - A')
∵ (A - A')' = - (A - A')
Thus, A - A' is a skew-symmetric matrix.

Question 9.
If A = $\left[\begin{array}{ccc}0& a& b\\ -a& 0& c\\ -b& -c& 0\end{array}\right]$, then find $\frac{1}{2}$ (A + A') and $\frac{1}{2}$ (A - A').
Answer:

Question 10.
Express the following matrices as the sum of a symmetric and a skew-symmetric matrix.
(i) $\left[\begin{array}{cc}3& 5\\ 1& -1\end{array}\right]$
Answer:
Let A = $\left[\begin{array}{cc}3& 5\\ 1& -1\end{array}\right]$
We know that any square matrix can be expressed as sum of symmetric and skew-symmetric matrices.
Here, A = $\left[\begin{array}{cc}3& 5\\ 1& -1\end{array}\right]$ then $\frac{1}{2}$ (A + A') will be symmetric and $\frac{1}{2}$ (A - A') will be skew-symmetric matrix.

(ii) $\left[\begin{array}{ccc}6& -2& 2\\ -2& 3& -1\\ 2& -1& 3\end{array}\right]$
Answer:

(iii) $\left[\begin{array}{ccc}3& 3& -1\\ -2& -2& 1\\ -4& -5& 2\end{array}\right]$
Answer: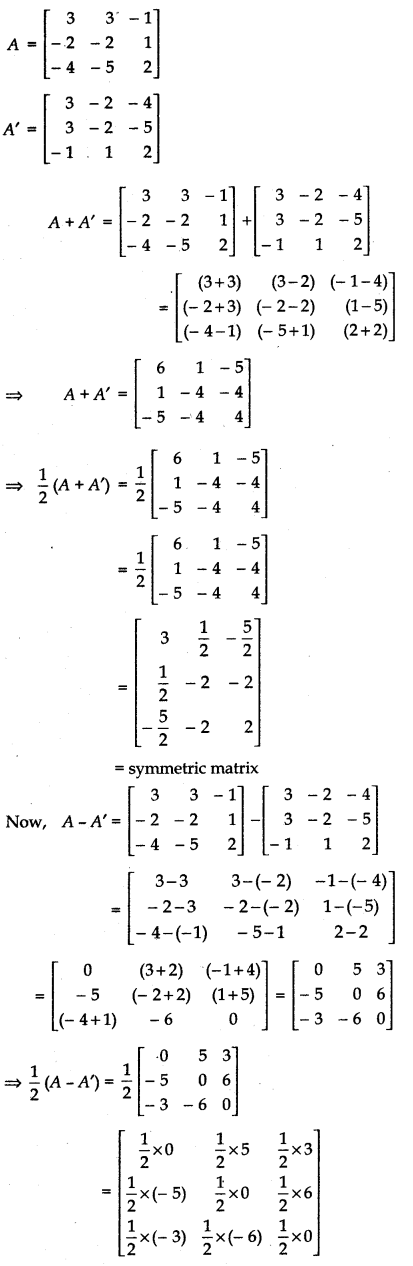

(iv) $\left[\begin{array}{cc}1& 5\\ -1& 2\end{array}\right]$
Answer:

Choose the correct answer in the exercises 11 and 12.

Question 11.
If A, B are symmetric matrices of same order, then AB - BA is a:
(A) Skew symmetric matrix
(B) Symmetric matrix
(C) Zero matrix
(D) Identity matrix
Answer:
Matrix A and B are symmetric matrix of equal order.
∴ A' = A, B' = B
(AB - BA)' = (AB)' - (BA)'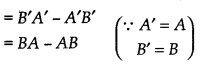

= - (AB - BA)
= skew-symmetric matrix
= (AB - BA) skew-symmetric matrix.
Thus, (A) is correct.

Question 12.
If A = $\left[\begin{array}{cc}\cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]$, then A + A' = I, then the value of α is:
(A) $\frac{\pi }{6}$
(B) $\frac{\pi }{3}$
(C) π
(D) $\frac{3\pi }{2}$
Answer:

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !