RBSE Class 12 Maths Solutions Chapter 3 Matrices Ex 3.2
Question 1.
Let
A = B = , C =
Find each of the following:
(i) A + B
Answer:
(ii) A - B
Answer:
(iii) 3A - C
Answer:
(iv) AB
Answer: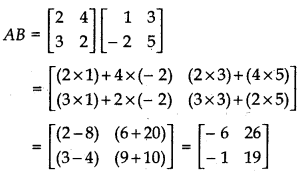
(v) BA
Answer:
Question 2.
Compute the following:
(i) +
Answer: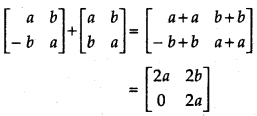
(ii)
Answer:
(iii)
Answer: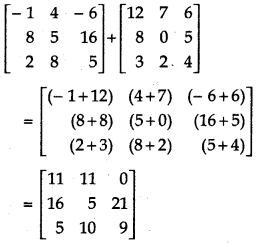
(iv)
Answer:
Question 3.
Compute the indicated products:
(i)
Answer:
(ii)
Answer: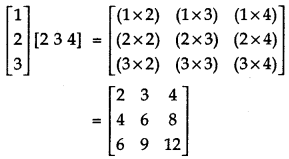
(iii)
Answer:
(iv)
Answer:
(v)
Answer: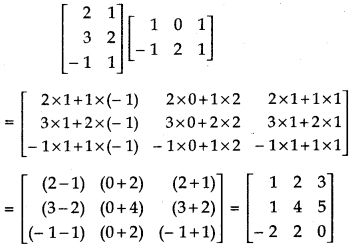
(vi)
Answer:
Question 4.
If A = , B = and C = , then compute (A + B) and (B - C). Also verify that A + (B - C) = (A + B) - C.
Answer:
Question 5.
If A = and B = then compute 3A - 5B.
Answer:
Question 6.
Simplify:
cos θ + sin θ
Answer:
Question 7.
(i) X + Y = and X - Y =
Answer:
(ii) 2X + 3Y = and 3X + 2Y =
Answer:
Question 8.
Find X if Y = and 2X + Y = .
Answer:
Question 9.
Find x and y if
2
Answer:
Comparing corresponding elements, we get
2 + y = 5,
⇒ y = 5 - 2,
⇒ y = 3,
∴ y = 3,
2x + 2 = 8
⇒ 2x = 8 - 2
⇒ 2x = 6
∴ x = 3
Question 10.
Solve the equation for x, y, z and t, if
2
Answer:
Comparing corresponding elements, we get
2x + 3 = 9, 2z - 3 = 15, 2y = 12, 2t + 6 = 18
⇒ 2x = 9 - 3, 2z = 15 + 3, y = , 2t = 18 - 6
⇒ 2x = 6, 2z = 18, y = 6, 2t = 12
∴ x = 3, z = 9, y = 6, t = 6
Question 11.
If x+ y = , then find the values of x and y.
Answer:
⇒ 2x - y = 10 ........ (i)
3x + y = 5 .......... (ii)
Adding equation (i) and (ii), we get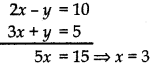
Putting value of x in euqation (i), we get
2 × 3 - y = 10 ⇒ 6 - y = 10
⇒ - y = 10 - 6 ⇒ y = 4
⇒ y = - 4
Thus, x = 3, y = - 4
Question 12.
Given
3
find the value of x, y, z and w.
Answer:
Comparing corresponding elements, we get
3x = x + 4,
3z = - 1 + z + w,
⇒ 3x - x = 4
⇒ 2x = 4,
3z - z = w - 1,
2z = w - 1,
3y = 6 + x + y
3w = 2w + 3
3y - y = 6 + x
2y = 6 + x
3w - 2w = 3
w = 3
∴ x = 2,
2y = 6 + 2, ⇒ 2y = 8,
y = 4
And w = 3, then 2z = w - 1
⇒ 2z = 3 - 1
⇒ 2z = 2
∴ z = 1
Thus, x = 2, y = 4, z = 1, w = 3
Question 13.
If F(x) = , show that F(x) F(y) = F(x + y).
Answer:
Question 14.
Show that
(i)
Answer:
(ii)
≠
Answer:
Question 15.
If A = , then find the value of A2 - 5A + 6I
Answer:
Here, A2 = AA
Question 16.
If A = , then prove that:
A3 - 6A2 + 7A + 2I = 0
Answer:

Question 17.
If A = and I = and A2 = KA - 2I, then find k.
Answer:
⇒ 1 = 3k - 2, - 2 = - 2k
4 = 4k, - 4 = - 2k - 2
⇒ 3k = 2 + 1, 2k = 2
4k = 4, - 2k = - 4 + 2
⇒ 3k = 3, 2k = 2
4k = 4, - 2k = - 2
⇒ k = 1, k = 1
Question 18.
If and I is the identity matrix of order 2, show that I + A = (I - A)
Answer:
Question 19.
A trust fund has ₹ 30,000 that must be invested in two different types of bonds. The first bond pays 5% interest per year and the second bond pays 7% interest per year. Using matrix multiplication determine how to divide ₹ 30,000 among the two types of bonds. If the trust fund must obtain an annual total interest of:
(a) ₹ 1,800
(b) ₹ 2,000
Answer:
Let x and (30000 - x) are two parts of ₹ 30,000.
Then matrix A = [x (30000 - x)]
Rate of interest are 5% and 7% or 0.05 and 0.07
Let matrix of rate R =
(a) We have, total interest = ₹ 1800
= [x (30000 - x)] = [1800]
⇒ [x × 0.05 + (30000 - x) × 0.07] - [1800]
⇒ [0.05x + (30000 × 0.07) - 0 07 × x] = [1800]
⇒ 0.05x + 2100 - 0.07× = 1800
⇒ 0.05x - 0.07x = 1800 - 2100
⇒ - 0.02x = - 300
⇒ x = = = 15000
First bond = ₹ 15,000
Now 30000 - x = 30000 -15000
∴ Second bond = ₹ 15,000
Thus, each bond should be bought for ₹ 15,000 so that interest of ₹ 1800 is received.
(b) For interest ₹ 2,000, matrix equation will be of the following type
[x (3000 - x)] = [2000]
⇒ [x × 0.05 + (30000 - x) × 0.07] = [2000]
⇒ [0.05x + (30000 × 0.07) - (x × 0.07]) = [2000]
⇒ 0.05x + 2100.00 - 0.07x = 2000
⇒ 0.05x - 0.07x = 2000 - 2100
⇒ - 0.02x = - 100
⇒ x = = = 5000
∴ First bond = ₹ 5,000
Thus 30000 - x = 30000 - 5000 = 25000
∴ Second bond = ₹ 25,000
To get ₹ 2,000 as interest two bonds should be divided into ₹ 5,000 and ₹ 25,000.
Question 20.
The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are ₹ 80, ₹ 60 and ₹ 40 each respectively. Find the total amount the book shop will receive from selling all the books using matrix algebra.
Answer:
Number of books in school is as follows:
Subject | Number of books |
Chemistry | 10 dozen = 10 × 12 = 120 |
Physics | 8 dozen = 8 × 12 = 96 |
Economics | 10 dozen = 10 × 12 = 120 |
Let number of books are represented by A
∴ A = [120 96 120]
And selling prices are represented by R then
∴ R =
Money obtained by selling the books
= AR = [120 96 120]
= [(120 × 80) + (96 × 60) + (120 × 40)]
= [9600 + 5760 + 4800] = [20160]
Total money obtained = ₹ 20,160
Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3 and p × k respectively. Choose the correct answer in exercises 21 and 22.
Question 21.
The restriction on n, k and p so that PY + WY will defined are:
(A) k = 3, p = n
(B) k is arbitary, p = 2
(C) p is arbitrary, k = 3
(D) k = 2, p = 3
Answer:
Order P matrix P = p × k
Order of martix Y = 3 × k
Order of matrix W = n × 3
Then for PY defined
Number of columns in P = number of rows in Y
k =3
and WY defined
Number of columns in W = number of rows in Y
(w = 3)
Now PY + WY defined
order of PY = p × k = p × 3
Then order of WY = n × k
Thus, PY + WY is defined if order of PY and WY are same
∴ p = n and k = 3
Thus (A) is correct.
Question 22.
If n = p, then order of matrix 7X - 5Z.
(A) p × 2
(B) 2 × n
(C) n × 3
(D) p × n
Answer:
X Order of X = 2 × n
Z Order of Z = 2 × p
∵ p = n
Thus, order of 7X - 5Z = 2 × n,
Hence, choice (B) is correct.
























Either way the teacher or student will get the solution to the problem within 24 hours.