RBSE Class 12 Maths Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.2

RBSE Class 12 Maths Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.2

Question 1.

3 sin-1 x = sin-1 (3x - 4x3), x ∈ $[-\frac{1}{2},\frac{1}{2}]$
Answer:
Let sin-1 x = θ ⇒ sin θ = x
∵ sin 3θ = 3 sin θ - 4 sin3θ
⇒ sin 3θ = 3x - 4x3
⇒ 3θ = sin-1(3x - 4x3)
Thus, 3 sin-1 x = sin-1 (3x - 4x3)
Hence Proved.

Question 2.
3 cos-1x = cos-1 (4x3 - 3x), x ∈ $[\frac{1}{2},1]$
Answer:
Let cos-1 x = θ ⇒ cos θ = x
⇒ cos 3θ = 4 cos 3θ - 3 cos θ
⇒ cos 3θ = 4x3 - 3x
⇒ 3θ = cos-1 (4x3 - 3x)
Thus, 3 cos-1 x = cos-1 (4x3 - 3x)
Hence Proved.

Question 3.
tan-1$\frac{2}{11}$ + tan-1$\frac{7}{24}$ = tan-1$\frac{1}{2}$
Answer:

Question 4.
2 tan-1$\frac{1}{2}$ + tan-1$\frac{1}{7}$ = tan-1$\frac{31}{17}$
Answer:

write the following functions in the simplest form:

Question 5.
tan-1$\frac{\sqrt{1+x^2}-1}{x}$, x ≠ 0
Answer:

Question 6.
tan-1$\frac{1}{\sqrt{x^2-1}}$, |x| > 1
Answer:

Question 7.
tan-1$\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)$, 0 < x < π
Answer:

Question 8.
tan-1$\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right),\frac{-\pi }{4}$ < x < $\frac{3\pi }{4}$
Answer:

Question 9.
tan-1 $\frac{x}{\sqrt{a^2-x^2}}$, |x| < a
Answer:

Question 10.
tan-1$\left\{\frac{3a^{2}x-x^3}{a^3-3a{x}^2}\right\}$, a > 0, - $\frac{a}{\sqrt{3}}$ < x < $\frac{a}{\sqrt{3}}$
Answer:

Find the values of each of the following:

Question 11.
tan-1$\left[2\cos \left(2{\sin }^{-1}\frac{1}{2}\right)\right]$.
Answer:

Question 12.
cot (tan-1 a + cot-1 a)
Answer:
We have, cot (tan-1 a + cot-1 a)
= cot $\frac{\pi }{2}$ = 0 (∵ tan-1 a + cot-1 a = $\frac{\pi }{2}$)
Hence, cot(tan-1 a + cot-1 a) = 0

Question 13.
$\tan \frac{1}{2}[{\sin }^{-1}\frac{2x}{1+x^2}+{\cos }^{-1}\frac{1-y^2}{1+y^2}]$, |x| < 1, y > 0 and xy > 1
Answer:

Question 14.
If sin(sin-1 $\left(\frac{1}{5}\right)$ + cos-1 x) = 1, then find the value of x.
Answer:

Question 15.
If tan-1$\left(\frac{x-1}{x-2}\right)$+ tan-1$\left(\frac{x+1}{x+2}\right)$ = $\frac{\pi }{4}$, then find value of x.
Answer:

Find the values of each of the expression in questions 16 to 18:

Question 16.
sin-1 (sin$\frac{2\pi }{3}$).
Answer:

Question 17.
tan-1 $\left(\tan \frac{3\pi }{4}\right)$
Answer:

Question 18.
tan $({\sin }^{-1}\frac{3}{5}+{\cot }^{-1}\frac{3}{2})$
Answer:

Question 19.
cos-1 $\left(\cos \frac{7\pi }{6}\right)$ is equal to:
(A) $\frac{7\pi }{6}$
(B) $\frac{5\pi }{6}$
(C) $\frac{\pi }{3}$
(D) $\frac{\pi }{6}$
Answer:
The principal value branch of cos-1 is [0, π].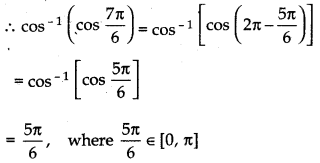

Thus, option (B) is correct.

Question 20.
sin [$\frac{\pi }{3}$-sin-1 $(-\frac{1}{2})$] is equal to:
(A) $\frac{1}{2}$
(B) $\frac{1}{3}$
(C) $\frac{1}{4}$
(D) 1
Answer:

Thus, option(D) is correct.

Question 21.
tan-1 √3 - cot-1 (- √3) is equal to:
(A) π
(B) - $\frac{\pi }{2}$
(C) 0
(D) 2√3
Answer:

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !