RBSE Class 12 Maths Solutions Chapter 1 Relations and Functions Ex 1.2

RBSE Class 12 Maths Solutions Chapter 1 Relations and Functions Ex 1.2

Question 1.

Show that the function f: R* → R* defined by f(x) = $\frac{1}{x}$ is one-one and onto, where R* is the set of all non-zero real numbers. Is the result true, if the domain R* is replaced by N with co-domain being same as R* ?
Answer:
Given function f(x) = $\frac{1}{x}$, f:R* → R*
Let x1, x2 ∈ R* (domain)
then f(x1) = f(x2) ⇒ $\frac{1}{x_1}=\frac{1}{x_2}$
⇒ x1 = x2
Thus, function is one one.
Again, if y is an arbitrary element of co-domain.
If f(x) = y, then
y = $\frac{1}{x}$ ⇒ x = $\frac{1}{y}$, y ≠ 0
which is an element of domain.
(∀ y ∈ R*, x ∈ R*)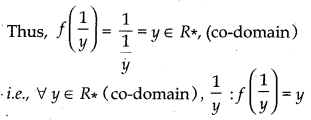

∴ f(R*) = R*
But each element of co-domain is image of one and only one element of domain.
∴ f is onto.
Thus, the given function is one-one and onto.

(ii) When domain R* is replaced by set of natural numbers N and co-domain remains R* then f: N → R*
and f(x) = $\frac{1}{x}$, where x ∈ N
If x1, x2 ∈ N, then
f(x1) = f(x2) ⇒ $\frac{1}{x_1}=\frac{1}{x_2}$
⇒ x1 = x2, x1, x2 ∈ N
∴ function f is one-one.
Since, domain is set of natural numbers and co-domain is set of non-zero rea1 "ambers, then
f:N → R* and f(x) = $\frac{1}{x}$
Let y ∈ R* (co-domain) is any arbitrary element, and f(x) = y

y = $\frac{1}{x}$ ⇒ x = $\frac{1}{y}$
Thus, range of f ⊂R*
Since, some elements of R* are not images of any element of domain.
∴ f is not onto.
So, f is one-one but not onto. Thus, by replacing R* by N result also changes.
Hence Proved.

Question 2.
Check the injectivity and surjectivity of the following functions:
(i) f: N → N given by f(x) = x2
(ii) f: Z → Z given by f(x) = x2
(iii) f:R → R given by f(x) = x2
(iv) f:N → N given by f(x) = x3
(v) f: Z → Z given by f(x) = x3
Answer:
(i) Function f: N → N is given by f(x) = x2
Let x1, x2 ∈ N then
f(x1) = f(x2) ⇒ x12 = x22
⇒ x1 = x2
So, function is (injective).
[x1 = ± x2, x2 cannot be - ve, since x2 ∈ N]
Again, in f(x) = x2 putting x = 1, 2, 3 .......
f(1) = 12 = 1
f(2) = 22 = 4
f(3) = 32 = 9
i.e., There exist some elements in co-domain which are not images of any element of domain. For example, if 5, exist in co-domain, then 5 is not the image of any element of domain. So, f is not onto. (Surjective)
∴ Range of f ⊂ N (co-domain)
∴ f is not onto.
Thus, f is injective but not surjective.

(ii) f: Z → Z, f(x) = x2
Let x1, x2 ∈ Z(domain), then
f(x1) = f(x2)
⇒ x12 = x22 (by definition off)
⇒ (x12 - x22) = 0
⇒ (x1 - x2) (x1 + x2) = 0
⇒ (x1 - x2) = 0 or (x1 + x2) = 0
⇒ x1 = x2 or x1 = - x1
∴ f(x1) = f(x2) ⇒ x1 ≠ x2 (∵ x1 = - x2)
Thus, f is not one-one.
Since x = 1 then f(1) = 12 = 1
then x = - 1 then f(- 1) = (- 1)2 = 1
∴ 1 ≠ - 1 ⇒ f(1) = f(-1) = 1
or f(1) = f(-1) ⇒ 1 ≠ (- 1)
Again, let y ∈ Z (co-domain) is any arbitrary element,
then y = x2 ⇒ x = ± √y (y > 0)
Thus, f is not onto.
Range of f ⊂ Z (co-domain)
∴ f is not onto (Surjective).
Since, in f(x) = x2 putting x = - 1, - 2, - 3, 1, 2, 3
f(1) = 12 = 1, f(- 1) = (- 1)2 = 2,
f(2) = 22 = 4, f(- 2) = (- 2)2 = 4,
f(3) = 32 = 9,
f(- 3) = (-3)2 = 9 etc.
i.e., There exist some elements in co-domain which are not image of any element of domain. For example 7, exist in co-domain but not image of any element of domain. So, f is not onto.
Thus, function is neither injective nor surjective.

(iii) f: R → R is given by f(x) = x3
If 1, - 1 ∈ R, (domain)
Then, f(1) = 12 ⇒ f(-1) = (- 1)2 = 1
Thus, 1 ≠ - 1 ⇒ f(1) = f(- 1)
Here two distinct elements of domain have same image.
∴ Function is not injective.
Again, we see that - 2, 3 are in co-domain but are not the images of any element of domain. Thus, f is not surjective.
∴ f is neither injective nor surjective.

(iv) f: N → N is given by f(x) = x3
If x1, x2 ∈ N domain, then
f(x1) = f(x2) ⇒ x13 = x23,
⇒ x1 = x2
We see that if images of two elements are same, then two elements are same.
Thus, f is injective.
Again, in N, co-domain of function/, there exist many elements which are not image of any one element of domain like 2, 3, 4, 5 etc.
Range of function f = {1, 8, 27, 64,...} ⊂ N
i.e. f(N) ⊂ N
Function is not surjective.
Thus, function is injective but not surjective.

(v) f: Z → Z is given by f(x) = x3
If x1, x2 ∈ Z (domain), then
f(x1) = f(x2) ⇒ x13 = x23
⇒ x1 = x2
Thus, f is injective.
Again, f(1) = 13 = 1, f(-1) = (-1)3 = - 1
f2) = 23 = 8, f(- 2) = (-2)3 = - 8
f(3) = 33 = 27, f(- 3) = (- 3)3 = - 27
f(4) = 43 = 64, f(- 4) = (- 4)3 = - 64
Thus, range of/.
= {..... - 64, - 27, -8, -1, 0,1, 8, 27, 64, ......} ⊂ Z
i.e. f(Z) ⊂ Z (co-domain)
∴ Function f is not surjective.
Thus, function f is injective but not surjective.

Question 3.
Prove that the Greatest Integer Function f:R → R, given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
Answer:
Given, function f: R → R and f(x) = [x] then,
f(1.4) = 1 and f(1.7) = 1
1.4 ≠ 1.7 ⇒ f(1.4) = f(1.7) = 1
Here, 1.4 and 1.7 both have image 1.
∴ f is not injective.
Since, co-domain of/is set of real numbers R and in the co-domain, all numbers are not integers. But image of x ∈ R (domain) is integer.
∴ The element of co-domain, which is not an integer, is not the image of any element of domain, i.e.,
f(R) ⊂ R (co-domain)
∴ f is not surjective.
Thus, f is neither injective nor surjective.
Hence proved.

Question 4.
Show that the Modulus Function f: R → R, given by f(x) = |x|, is neither one-one nor onto, where |x| is x, if x is positive or 0 and |x| is - x, if x is negative.
Answer:
Here f: R → R and f(x) = |x|, then
f(1) = |1| = 1 and f(- 1) = |- 1| = 1
Here 1 ≠ - 1 ⇒ f(1) = f(- 1) = 1
i.e., Image of two elements 1 and -1 of domain is same as 1.
∴ f is not injective.
f(o) = o
Again f(1) = | 1 | = 1,
f(- 1) = |- 1| = 1
f(2) = |2| = 2,
f(3) = |3|= 3,
f(- 3) = |- 3| = 3
f(4) = |4| = 4,
f(- 4) = |- 4| = 4
Since, there are negative numbers also in co-domain of f but any negative number of co-domain is not the image of any element of domain of f.
∴ f is not surjective.
Thus, function f is neither injective nor surjective.
Hence Proved.

Question 5.
Show that the Signum Function f: R → R, given by

is neither one-one nor onto.
Answer:
Here f: R → R, and

Here, f(1) = 1, f(2) = 1, since 1 > 0, 2 > 0
∴ 1 ≠ 2 ⇒ f(1) = f(2)
i.e., two elements of domain 1 and 2, have same image 1.
Function is not injective.
Since, co-domain of function is set of real numbers and - 1, 0, 1 is only image of elements of domain, then
f(R) = { -1, 0, 1} ⊂ R (Co-domain)
Range of f = {- 1, 0, 1} ⊂ R (Domain)
∴ f is not surjective.
Thus, function f is neither injective nor surjective.
Hence Proved.

Question 6.
Let A = {1, 2, 3}, B = {4, 5, 6, 7} and let f = (1, 4,), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Answer:
According to the questions,
A = {1, 2, 3}, B = {4, 5, 6, 7}
f: A → B is such that
f = {(1, 4), (2, 5), (3, 6)}
Then f(1) = 4, f(2) = 5, f(3) = 6
i.e., Each elements of A has distinct image.
Thus, f is injective.
This can be shown as follows:

Hence Proved.

Question 7.
In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.
(i) f: R → R defined by f(x) = 3 - 4x
(ii) f: R → R defined by f(x) = 1 + x2
Answer:
(i) Here, f: R → R and f(x) = 3 - 4x
If x1, x2 ∈ R domain, then
f(x1) = f(x2) ⇒ 3 - 4x1 = 3 - 4x2
⇒ - 4x1 = - 4x2
⇒ x1 = x2
∴ f is injective.
Again, if y is any arbitrary element of co-domain such that f(x) = y
then y = 3 - 4x ⇒ y - 3 = - 4x

Thus, each element of co-domain is image of any element of domain necessarily.
∴ f is surjective.
Thus, f is one-one and onto.

(ii) f: R → R and f(x) = 1 + x2
Let x1, x2 ∈ R (domain), then,
f(x1) = f(x2) ⇒ 1 + x12 = 1 + x22
⇒ x12 = x22
⇒ (x12 - x22) = 0
⇒ (x1 - x2) (x1 + x2) = 0
⇒ x1 = x2 or x1 = - x2
i.e,, Being images of elements equal, elements are not equal.

Example: f(1) = 1 + 12 = 2
f(- 1) = 1 + (- 1)2
= 1 + 1 = 2
i.e„ 1 ≠ - 1
⇒ f(1) = f(- 1) = 2
∴ f is not injective.
Co-domain of function f has negative numbers also which are not image of any element of domain.
∴ f is not surjective.
Let y ∈ R (co-domain), then
f(x) = y = 1 + x2
⇒ x2 = y - 1
then x = ± √y - 1
If y = 0, then x = ± √-1 ∉ R
So, f is not surjective.
Thus, function f is neither injective nor surjective.

Question 8.
Let A and B be sets. Show that f: A × B → B × A such that f(a, b) = (b, a) is bijective function.
Answer:
According to question,
f: A × B → B × A if f(a, b) = (b, a)
Let (a1, b1) and (a2, b2) ∈ A × B, then
f(a1, b1) = f(a2, b2)
⇒ (b1, a1) = (b2, a2)
⇒ b1 = b2 , a1 = a2
⇒ (b1, a1) = (b2, a2)
Thus, f(a1, b1) = f(a2, b2)
⇒ (b1, a1) = (b2, a2)
where (a1, b1), (a2, b2) ∈ A × B
∴ Function f is injective.
Again, let (b, a) be an arbitrary element of set B × A, then (F, a) ∈ B × A.
⇒ b ∈ B and a ∈ A
⇒ a ∈ A and b ∈ B
⇒ (a, b) ∈ A × B
Thus, ∀ (b, a) ∈ B × A ∃ (a, b) ∈ A × B is such that
f(a, b) = {a, b)
∴ f: A × B → B × A is surjective.
Thus, given function is bijective function.
Hence Proved.

Question 9.
Let f: N → N be defined by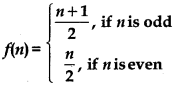

for all n ∈ N. State whether the function f is bijective. Justify your answer.
Answer:
f: N → N and

i.e., Image of two distinct elements 1 and 2 is same as element 2.
Thus, function is not one-one, i.e., function is many-one. Let n be any arbitrary constant of set N, i.e., n ∈ N.
If n is odd then (2n - 1) will also be odd, then
f(2n - 1) = $\frac{(2n-1)+1}{2}$ = $\frac{2n}{2}$ = n
f(n) = $\frac{(n-1)}{2}$, when n is odd
and when n is even then 2n will also be even.
Thus, f(2n) = $\frac{2n}{2}$ = n [∵ f(n) = $\frac{n}{2}$, when n os even]
Thus, we see that either n is even or odd.
Then f(N) = N
∴ f is surjective.
Thus, given function is many-one onto but not one-one onto.

Question 10.
Let A = R - {3} and B = R - {1}. Consider the function f: A → B defined by f(x) = $\left(\frac{x-2}{x-3}\right)$. Is f one-one and onto ? Justify your answer.
Answer:
According to the question,
A = R - {3} and B = R - {1} and f: A → B, then
f(x) = $\frac{x-2}{x-3}$
Let x1, x2 ∈ A, then
Let f(x1) = f(x2) ⇒ $\frac{x_1-2}{x_1-3}=\frac{x_2-2}{x_1-3}$
⇒ (x1 - 2) (x2 - 3) = (x2 - 2) (x1 - 3)
⇒ x1x2 - 3x1 - 2x2 + 6 = x1x2 - 3x2 - 2x1 + 6
⇒ 3x2 - 2x2 = 3x1 - 2x1
⇒ x2 = x1
⇒ x1 = x2
∴ Function f is one-one.
Again, let y ∈ B be any arbitrary elements such that
y = f(x)
y = $(\frac{x-2}{x-3},x\ne 3)$
then (x - 3) y = x - 2
⇒ xy - 3y = x - 2
⇒ xy - x = 3y -2
⇒ x(y - 1) = 3y - 2
∴ x = $\frac{3y-2}{y-1}$
Clearly, x is not defined for y ≠ 1.

Thus, ∀ y ∈ B, ∃ x ∈ A: f(x) = y
∴ Function f is onto.
Thus, given function f is one-one onto.

Question 11.
Let f: R → R be defined as f(x) = x4. Choose the correct answer:
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto
Answer:
According to the question,
f:R → R, f(x) = x4
Let x1, x2 ∈ R (domain)
∴ f(x1) = f(x2)
⇒ x14 = x24
⇒ x14 - x24 = 0
⇒ (x12 - x22) (x12 + x22) = 0
But x12 + x12 ≠ 0, since sum of squares of two real numbers cannot be zero.
∴ x12 - x22 = 0
⇒ (x1 - x2) (x1 + x2) = 0
⇒ x1 - x2 = 0 or x1 + x2 = 0
⇒ x1 = x2 or x1 = - x2
f(x1) = f(x2) ⇒ x1 ≠ x2,
Thus, f is not one-one.
Since, x = 1 for, f(1) = 14 = 1
and x = - 1 for, f(- 1) = (- 1)4 = 1
and x = 2 for f(2) = 24 = 16
and x = - 2 for, f(- 2) = (- 2)4 = 16
i.e., f(1) = f(-1) and f(2) = f(- 2)
∴ 1 ≠ - 1 ⇒ f(1) = f(- 1) = 1
and 2 ≠ - 2 ⇒ f(2) = f(- 2) = 16
For onto, let y ∈ R (co-domain) be any arbitrary element.
and f(x) = y
then , y = x4 ⇒ x = (y)1/4, y ≥ 0
∵ There are negative numbers also in co-domain. Thus, any negative number (of co-domain) is not the image of any element of domain. For example, element - 2 of co-domain is not the image of any element of domain. In other words, range of f is set of non-negative numbers, i.e.,
Range of f ⊂ R (co-domain)
So, function is not onto.
Thus, given function is neither one-one nor onto and so, (D) is correct.

Question 12.
Let f: R → R be defined as f(x) = 3x. Choose the correct answer:
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto
Answer:
According to the question,
f: R → R, if f(x) = 3x .
Let x1, x2 ∈ R (domain)
Then f(x1) = f(x2) ⇒ 3x1 = 3x2
⇒ x1 = x2
Thus, f is one-one.
Let y ∈ R co-domain be any arbitrary element such that y = f(x), then
y = f(x) ⇒ y = 3x

Thus, image of $\frac{y}{3}$ element of domain R is element y of co-domain.
∴ f is onto
So, function is one-one onto.
Thus, (A) is correct.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !