RBSE Class 12 Maths Solutions Chapter 1 Relations and Functions Ex 1.1

 RBSE Class 12 Maths Solutions Chapter 1 Relations and Functions Ex 1.1

Question 1.
Determine whether each of the following relations are reflexive, symmetric and transitive :
(i) Relation R in the set A = {1, 2, 3, ..., 13, 14} defined as
R = {(x, y): 3x - y = 0}
Answer:
According to question,
A = {1, 2, 3, ......... 13, 14}
and R = {(x, y): 3x - y = 0}

(a) R = {(x, y):3x - y = 0}
Putting y = x
3x - x = 2x ≠ 0
So, xRx is not true. [∵ x ≠ 0]
i.e., (x, x) ∈ R
Thus, R is not reflexive.

 

(b) Interchanging x and y,
If 3x - y = 0
then 3y - x ≠ 0
So, xRy ⇏⇏ yRx
i.e., (x, y) ∈ R ⇏⇏ (y, x) ∈ R
This, R is not symmetiric.

(c) If 3x - y = 0 and 3y - z = 0, then
On adding
3x - y + 3y - z = 0 + 0
3x - z = - 2y
So, 3x - z ≠ 0
i.e., (x, y) ∈ R, (y, z) ∈ R ⇏⇏ (x, z) ∈ R
Thus, R is not transitive.
Thus, R is not reflexive, symmetric and transitive.

(ii) Relation R in the set N of natural numbers defined as
R = {(x, y): y = x + 5 and x < 4}
Answer:
Set of natural numbers
N = {1, 2, 3, 4, ......... }
R = {(x, y): y = x + 5 and x < 4}
then R = {(1, 6), (2, 7), (3, 8)}

(a) Here (x, x) ∉ R so xRx is not true.
Thus, P is not reflexive.

 

(b) Again, interchanging x and y
y = x + 5 ⇏⇏ x = y + 5
(1, 6) ∈ P ⇏⇏ (6, 1) ∈ R
or (x, y) ∈ R ⇏⇏ (y, x) ∈ R
So, R is not symmetric.

(c) In relation P = {(1, 6), (2, 7), (3,8)}
In ordered pair (1, 6) and (2, 7), 6 ≠ 2
In ordered pair (2, 7) and (3,8), 7 ≠ 3
Thus, we see that (x, y) ∈ R but (y, z) ∉ P, then (x, z) ∈ R
⇒ P is not transitive.
Thus, R is not reflexive, symmetric and transitive.

(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6) as
R = {(x, y): y is divisible by x}
Answer:
According to question,
A = {1, 2, 3, 4, 5, 6}
and R = {(x, y): y, is divisible by x}
Thus, R = {(1,1), (1,2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6)}

(a) Here, P is reflexive since xPx is true.
Since, (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) all ordered pairs are in R.

 

(b) Again, y is divisible by x but number x is not divisible by y, as
(2, 4) ∈ R but (4, 2) ∈ R
i.e., (x, y) ∈ ⇏⇏ (y, x) ∈ R
Thus, P is not symmetric.

(c) (1, 2) ∈ R and (2, 4) ∈ R ⇒ (1, 4) ∈ R
Similarly, (1, 3) ∈ R, (3, 6) ∈ R ⇒ (1, 6) ∈ R
i.e., (x, y) ∈ R, (y, z) ∈ R ⇒ (x, z) ∈ R
So, P is transitive.
Thus, we see that P is reflexive and transitive but not symmetric.

(iv) Relation R in the set Z of all integers defined as
R = {(x, y): x - y is an integer}
Answer:
Set of all integers
Z = {......... - 3, - 2, - 1, 0, 1, 2, 3, ..........}
and P = {(x, y): x - y is an integer}

(a) In x - y putting x = y
x - x = 0, which is an integer
i.e., xRx is true
or (x, x) ∈ R, ∀ x ∈ Z
Thus, R is reflexive.

 

(b) Again, x - y is an integer then - (x - y) will also be an integer. [- ve of integer]
or y - x is also an integer
or (x, y) integer ⇒ (y - x) integer
or xRy ⇒ yRx, is true
or (x, y) ∈ R ⇒ (y, x) ∈ R
[since by taking x = 1, y = 2, 1 - 2 = - 1 (integer)
and 2 - 1 = 1 (integer)]
Thus, R is symmetric.

(c) If x - y and y - z both are integers.
So, x - y + y - z = x - z will also be integer.
[Sum of integers is also integer]
or xPy and yRx ⇒ xRz
So, R is transitive.
Thus, R is reflexive, symmetric and transitive.

(v) Relation R in the set A of human beings in a town at a particular time given by.
(a) R = {(x, y): x and y work at the same place}
(b) R = {(x, y): x and y live in the same locality}
(c) R = {(x, y): x is exactly 7 cm taller than y}
(d) R = {x, y): x is wife of y}
(e) R = {(x, y) :x is father of y}
Answer:
(a) R = {(x, y): x and y work at same place}

(i) R is reflexive, since each person work at same place at specific time, i.e., xRx is true.
or (x, x) ∈ R

(ii) R is symmetric, since x, y work at same place and at same time so we can say that y and x are also work at same place.
i.e., xRy ⇒ yRx
(x, y) ∈ R ⇒ (y, x) ∈ R

 

(iii) R is transitive, since x, y and y, z work at same place and at same time, then x, z work at the same place and at the same time i.e.,
xRy and yRz ⇒ xRz
or (x, y) ∈ R, (y, z) ∈ R ⇒ (x, z) ∈ R
Thus, R is reflexive, symmetric and transitive.

(b) R = {{x, y): x and y live in same colony}
(i) R is reflexive, since each person of this colony live in same colony.
i.e., xRx or (x, x) ∈ R

(ii) R is symmetric, since x and y live in same colony then y and x also live in same colony.
i.e., xRy ⇒ yRx
or (x, y) ∈ R ⇒ (y, x) ∈ R

(iii) R is transitive, since x and y, y, and z live at same place (colony) then x and z also live in same colony, i.e.,
xRy and yRz ⇒ xRz
or (x, y) ∈ R, (y, z) ∈ R ⇒ (X, Z) ∈ R
Thus, R is reflexive, symmetric and transitive.

 

(c) R = {(x, y): x is 7 cm longer than y}
(i) R is not reflexive, any person cannot be 7 cm longer than himself, i.e., xRx is not true.
or (x, x) ∉ R

(ii) R is not symmetric, since if x is 7 cm longer than y then y cannot be 7 cm longer than x.
i.e., xRy ⇏⇏ yRx
or (x, y) ∈ R ⇏⇏ (y, x) ∈ R

(iii) R is not transitive, since if x is 7 cm longer than y, and y is 7 cm longer than z then x cannot be 7 cm longer than z, i.e.,
xRy and yRz ⇏⇏ xRz
or (x, y) ∈ R, (y, z) ∈ R ⇏⇏ (x, z) ∈ R

(d) R = {(x, y): x is wife of y}
(i) R is not reflexive since any person cannot be wife of himself, i.e.,
xRx, is not true
or (x, x) ∉ R

(ii) R is not symmetric, if x is wife of y then y cannot be wife of x, i.e.,
xRy ⇏⇏ yRx
or (x, y) ∈ R ⇏⇏ (y, x) ∈ R

(iii) R is not transitive, since if x is wife of y then y cannot be wife of anyone, i.e., xRy then yRz then xRz or (x, y) ∈ R then (y, z) ∈ R and (x, z) ∈ R.
Thus, R is not reflexive, symmetric and transitive.

(e) R = {(x, y): x is father of y}
(i) R is not reflexive since no one can be father of himself i.e.,
xRx is not true
or (x, x) ∉ R

 

(ii) R is not symmetric, since if x is father of y then i/ cannot be father of x, i.e.
xRy ⇏⇏ yRx
or (x, y) ∈ R ⇏⇏ (y, x) ∈ R

(iii) R is not transitive, since x is father of y and y is father of z then x cannot be father of z.
i.e., xRy and yRz ⇏⇏ xRz
or (x, y) ∈ R, (y, z) ∈ R ⇏⇏ (x, z) ∈ R
Thus, R is not reflexive, symmetric and transitive.

Question 2.
Show that the relation R in the set R of real numbers, defined as R = {(a, b): a ≤ b²} is neither reflexive nor symmetric nor transitive.
Answer:
R = Set of real numbers
R = {(a, b): a ≤ b²}

(i) ∀ a ∈ R (R is a set of real numbers)
a ≰ a²
∴ (a, a) ∉ R
∴ R is not reflexive.

For example: $\frac{1}{3}$ is a real number and $\frac{1}{3}\le {\left(\frac{1}{3}\right)}^2$ is not true, i.e., $\frac{1}{3}$ R $\frac{1}{3}$ is not true or $(\frac{1}{3},\frac{1}{3})$ ∉ R.

(ii) aRb ⇒ a ≤ b²
⇒ b ≰ a²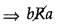

∴ (a, b) ∈ R ⇒ (b, a) ∉ R
∴ R is not symmetric.

For example:

Thus, R is not symmetric.

 

(iii) aRb and bRc ⇒ a ≤ b² and b ≤ c²
⇒ a ≤ c⁴ ⇒ a ≰ c²
∴ (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∉ R
∴ R is not transitive.

For example, consider real numbers 3, -3 and 1. Clearly,
3 ≤ (- 3)² and - 3 ≤ (1)²,
but 3 ≤ 1², is not true
i.e., (3, - 3) ∈ R and (- 3, 1) ∈ R but (3, 1) ∉ R
Thus, R is not transitive.

Question 3.
Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = [(a, b): b = a + 1} is reflexive, symmetric or transitive.
Answer:
Let A = {1, 2, 3, 4,5, 6}
and R = {(a, b): b = a + 1}

(i) R is not reflexive, since
a ≠ a + 1
i.e., aRa is not true.

(ii) R is not symmetric, since b = a + 1, then a ≠ b + 1
i.e., aRb ⇏ bRa
or (a, b) ∈ R ⇏ (b, a) ∈ R

 

(iii) R is not transitive since if b = a + 1, c = b + 1, then c ≠ a + 1
i.e., (a, b) ∈ R, (b, c) ∈ R ⇏ (a, c) ∈ R
or aRb, bRc ⇏ aRc
Thus, R is not reflexive, symmetric and transitive.

Question 4.
Show that the relation R in R defined as R = {(a, b): a ≤ b), is reflexive and transitive but not symmetric.
Answer:
In the set of real numbers relation R is defined as
R = {(a, b): a ≤ b}

(i) Relation R is reflexive, since for any real number.
a ≤ a ⇒ (a, a) ∈ R
Thus, aRa is true.

(ii) Relation R is transitive, since for real numbers a, b and c,
a ≤ b, b ≤ c ⇒ a ≤ c
i.e., (aRb) and (bRc) ⇒ aRc
or (a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∈ R

(iii) R is not symmetiric, since for any two real numbers a and b,
a ≤ b ⇏ b ≤ a
i.e., aRb ⇏ bRa
Thus, (a, b) ∈ R ⇏ (b, a) ∈ R
As (3, 4) ∈ R ⇒ 3 < 4
but 4 < 3 or (4, 3) ∉ R
Thus, R is reflexive and transitive but not symmetiric.

 

Questin 5.
Check whether the relation R in R defined by R = {(a, b): a ≤ b³} is reflexive, symmetric or transitive.
Answer:
Given relation, R = {(a, b) : a ≤ b³} where a and b are real numbers.

(i)

(ii) aRb ⇒ a ≤ b³ ⇒ b ≰ a³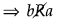

∴ (a, b) ∈ R ⇒ (b, a) ∉ R
∴ R is not symmetric.

For example:
For real numbers 1414 and 1

(iii) aRb and bRc
⇒ a ≤ b³ and b ≤ c³
⇒ a ≤ c⁹ ⇒ a ≰ c³
∴ (a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∉ R
∴ R is not transitive.

For example: Consider real numbers 5, 2 and $\sqrt[3]{32}$.
∵ 5 ≤ 23 is true ⇒ (5, 2) ∈ R
Again 2 ≤ (21/3)3 is true ⇒ (2, 21/3) ∈ R
But 5 ≰ (21/3)3 ⇒ (5, $\sqrt[3]{32}$) ∉ R
Thus, given relation is not transitive for all real numbers.
Thus, relation R is not reflexive, symmetric and transitive.

 

Question 6.
Show that the relation R in the set [1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
Answer:
(i) Relation R = {(1, 2), (2, 1)}, is not reflexive, since ordered pair (1, 1), (2, 2), (3, 3) does not exist in relation R.
(1, 1), (2, 2), (3, 3) ∉ R
or 1R1, 2R2 and 3R3 are not true

(ii) R = {(1, 2), (2, 1)} is symmetric, since
(1, 2) ∈ R ⇒ (2, 1) ∈ R
or 1R2 ⇒ 2R1

(iii) R = {(1, 2), (2,1)} is not transitive since R has only two elements (1, 2) and (2,1)
Thus, relation R is neither reflexive nor transitive but it is symmetric.
Hence Proved.

Question 7.
Show that the relation R in the set A of all the books in a library of a college given by R = {(x, y): x and y have same number of pages} is an equivalence relation.
Answer:
Let A = {x : x, books in a library of any college}
Given relation R = {(x, y) : Number of pages in x and y are same}
(i) Given relation R is reflexive since if x is any book then x and x will contain same pages i.e., for all x ∈ A.
xRx is true.

(ii) Relation R is symmetric, since if x, y ∈ A, then (x, y) ∈ R
⇒ Number of pages in x and y are same.
⇒ In x and y number of pages are same and in y and z number of pages are same.
⇒ (y, x) ∈ R
So, (x, y) ∈ R ⇒ (y, x) ∈ R

(iii) Let x, y, z ∈ A and (x, y) ∈ R, (y, z) ∈ R
Then (x, y) ∈ R, (y, z) ∈ R
⇒ [In x and y number of pages are same] and [in y and z number of pages are same.]
⇒ In x and z number of pages are same.
⇒ (x, z) ∈ R
So, (x, y) ∈ R, (y, z) ∈ R ⇒ (x, z) ∈ R ,
Thus, R is an equivalence relation.
Hence Proved.

 

Question 8.
Show that the relation R in the set A = {1, 2, 3, 4, 5} given by R = {(a, b): |a - b| is even} is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of [2, 4].
Answer:
Given relation R = {(a, b): |a - b| is even}
where a, b ∈ A and A = {1, 2, 3, 4, 5}

(i) R is reflexive, since |a - a| = 0, which is even.
(a, a) ∈ R
⇒ aRa is true.

(ii) R is symmetric, since (a, b) ∈ R, then
(a, b) ∈ R ⇒ |a - b| is even
⇒ |- (a - b)| is also even
[∵ |x| = |- x|]
⇒ |b - a | is even
⇒ (b, a) ∈ R
i.e., (a, b) ∈ R ⇒ (b, a) ∈ R is true.

(iii) R is transitive, since for real numbers a, b and c, if (a, b) ∈ R and (b, c) ∈ R, then (a, b) ∈ R, (b, c) ∈ R
⇒ |a - b| is even and |b - c| is even.
⇒ |a - b| and |b - c| are even.
⇒ a - b + b - c is also even
[sum of even numbers is also even]
⇒ a - c is also even
⇒ |a - c| is also even
⇒ (a, c) ∈ R
Thus, (a, b) ∈ R, (b, c) ∈ R
⇒ (a, c) ∈ R
⇒ aRb and bRc = aRc
We see that relation R is reflexive, symmetric and transitive. Thus, R is an equivalence relation.
Again, on set [1, 3, 5],
|1 - 3| = | - 2 | = 2, is an even number
|3 - 5| = | - 2 | = 2, is an even number
|1 - 5| = | - 4| = 4, is an even number
Thus, in {1, 3 , 5} all elements are related to each other, since elements of set [1, 3, 5] verify the given condition.
Similarly, on set {2, 4}
|2 - 4| = |- 2| = 2 is even
|4 - 2| = |2| = 2 is even
Thus, all elements of set {2, 4} are related to each other since elements of set {2, 4} verify the given condition.
Now, elements of set {1, 3, 5} and set {2, 4} are not related to each other because their elements did not verify given condition.
i.e., |1 - 2| = |- 1| = 1, which is an not even number
|3 - 4| = | - 1| = 1, which is not an even number
|5 - 2| = | 3 | = 3, which is not an even number
|5 - 4| = |1| = 1, which is not an even number
Hence Proved.

 

Question 9.
Show that each of the relation R in the set A = {x ∈ Z: 0 ≤ x ≤ 12} given by
(i) R = {(a, b): |a - b| is a multiple of 4}
(ii) R = {(a, b):a = b}
is an equivalence relation. Find the set of all elements related to 1 in each case.
Answer:
Given set
A = {x ∈ Z: 0 < x < 12}
or A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
(i) R = {(a, b): |a - b|, is multiple of 4}
Thus, R = {(0, 0), (0, 4), (0, 8), (0, 12), (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7), (8, 8), (9, 9), (10, 10), (11, 11), (12, 12), (1, 5), (1, 9), (2, 6), (2, 10), (3, 7), (3, 11), (4, 8), (4, 12), (5, 9), (6, 10), (7, 11), (8, 12)}

(a) R is reflexive since for any a e A
|a - a| = 0
which is a multiple of 4 since 0 × 4 = 0
⇒ (a, a) ∈ R
⇒ aRa is true.

(b) R is symmetric, since for a,b ∈ A
(a, b) ∈ R
⇒ |a - b|, is a multiple of 4
⇒ |a - b| = 4k, where k is a natural number
⇒ |- (b - a) | = 4k, where k is a natural number
⇒ |b - a| = 4k, where k is a natural number
⇒ (b, a) ∈ R
Thus, (a, b) ∈ R ⇒ (b, a) ∈ R
⇒ aRb ⇒ bRa.

(c) R is transitive, since for a, b, c ∈ A
If (a, b) ∈ R and (b, c) ∈ R
⇒ |a - b|, is a multiple of 4 and |b - c|, is a multiple of 4.
⇒ | a - b | = 4m and |b - c| = 4n,
where m and n are natural numbers.
⇒ a - b = ± 4 m and b - c = ± 4n
⇒ a - b + b - c = ± 4 m + (± 4n)
⇒ (a - c) = ± 4m + (± 4n)
⇒ ± 4(m + n), is a multiple of 4
⇒ |a - c| = 4k, is a multiple of 4
If k = m + n and k is a natural number.
⇒ (a, c) ∈ R
Hence, (a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∈ R
⇒ aRb and bRc ⇒ aRc
We see that relation R, according to given condition in given set is reflexive, symmetric and transitive.
Thus, relation R is an equivalence relation on set A.
Again let, |1 - x| ∈ R then |1 - x|, is a multiple of 4.
⇒ |1 - x| = 0, 4, 8, 12 ∈ A
⇒ When x = 1, then |1 - 1 | = 0, which is a multiple of 4.
When x = 5, then |1 - 5| = |- 4|=4, which is a multiple of 4.
When x = 9, then |1 - 9| = |- 8 | = 8, which is a multiple of 4.
∴ x = 1, 5, 9
Thus, set {1, 5, 9} is set of elements of set A which are related to 1 by R.

(ii) R = {(a, b):a = b}
and A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
Thus, R = {(0 ,0), (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7), (8, 8), (9, 9), (10, 10), (11, 11), (12, 12)}

(a) R is reflexive, since
a = a ⇒ (a, a) ∈ R
So, aRa, is true.

(b) R is symmetric, since for a, b ∈ A
If (a, b) ∈ R ⇒ a = b ⇒ b = a
⇒ (b, a) ∈ R
Thus, (a, b) ∈ R
⇒ (b, a) ∈ R, is true
So, aRb ⇒ bRa, is true

(c) R is transitive, since for a,b, c ∈ A
(a, b) ∈ R and (b, c) ∈ R
⇒ a = b and b = c
⇒ a = b = c
⇒ a = c
⇒ (a, c) ∈ R
Thus, (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R, is true
or aRb and bRc ⇒ aRc, is true.
We see that relation R in given set A, according to condition is reflexive, symmetric and transitive. Thus, R is an equivalence relation on set A. Again, set related to 1 (according to condition) is {1}. Hence Proved.

 

Question 10.
Give an example of a relation which is
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
Answer:
(i) Let A = Set of straight lines in a plane or A = {x : x, is a line in plane}
and relation R is defined on set A, such that
R = {(a, b): line a is perpendicular to b}

(a) Relation R is not reflexive because no line is perpendicular to itself, i.e.,
(a, a) ∉ R or aRa, is not true

(b) Relation R is symmetric, since line a is perpendicular to b means line b will be perpendicular to line a (since angle between two lines is 90°), i.e.,
(a, b) ∈ R ⇒ (b, a) ∈ R, is true
or aRb ⇒ bRa, is true

(c) Relation R is not transitive, since if line a is perpendicular to b and line b is perpendicular to line c then line a cannot be perpendicular to line c. Line a will be parallel to line c, i.e.,
(a, b) ∈ R, (b, c) ∈ R ⇏ (a, c) ∈ R
⇒ aRb and bRt ⇏ aRc
which is clear by the following figure:

Here a

⊥ b and b ⊥ c
Now a || c
Thus, relation R = {(a, b): line a is perpendicular to line b} is symmetric but not reflexive and transitive.

(ii) Let set A = Set of real numbers
or A = {x : x, is a real number}
and relation R is defined on set A, such that
R = {(a, b): a > b, where a and b are real numbers}

(a) R is transitive, since for a, b, c ∈ A
If a > b and b > c ⇒ a > c i.e.,
(a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R
or aRb and bRc ⇒ aRc
As 5 > 4, 4 > 3 then 5 > 3

(b) R is not reflexive since no number exceeds itself,
i.e., a > a is not true.
or aRa, is not true
or (a, a) ∉ R

(c) R is not symmetric, since for a, b ∈ A
If number a is greater than b, then number b cannot be greater than a, i.e.,
a > b ⇏ b > a
or (a, b) ∈ R ⇏ (b, a) ∈ R
or aRb ⇏ bRa
Thus, relation R = {(a, b): a > b, where a and b are real numbers} is transitive but not reflexive and symmetric.

(iii) Let A = {1, 2, 3, 4} and relation R on set A is defined such that
R = {(a, b): a + b ≤ 5, when a, b ∈ A}
or R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1)}
(a) R is reflexive, since (1, 1), (2, 2) ∈ R
i.e., 1R1,2R2, is true.
(b) R is symmetric, since (1, 2), (2, 1) ∈ R, (1, 3), (3 ,1) ∈ R and (1, 4), (4, 1) ∈ R
i.e., 1R2 ⇒ 2R1
1R3 ⇒ 3R1
1R4 ⇒ 4R1, is true

 

(c) R is not transitive, since if (2, 1) ∈ R, (1, 4) ∈ R but (2, 4) ∉ R, i.e.,
2R1 and 1R4 ⇏ 2R4
Thus, relation R = {(a, b) : a + b ≤ 5, where a, b e A} is reflexive and symmetric but not transitive.

(iv) Let A = {1, 2, 3, 4} and relation R is defined on set A, such that
R = {(a, b): a ≤ b)
R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}

(a) R is reflexive, since
(1, 1), (2, 2), (3, 3), (4, 4) ∈ R
i.e., 1R1, 2R2, 3R3, 4R4, are true.

(b) R is transitive, since
(1, 2), (2, 3) ∈ R ⇒ (1, 3) ∈ R
(1, 3), (3, 4) ∈ R ⇒ (1, 4) ∈ R
i.e., 1R2, 2R3 ⇒ 1R3
and 1R3 and 3R4 ⇒ 1R4

(c) R is not symmetric, since if number a is smaller than number b, then number b will not be smaller than number a.
As 1 < 2, then 2 ≰ 1
i.e., 1R2 ⇏ 2R1
or (1, 2) ∈ R ⇏ (2, 1) ∈ R
Thus, relation R = [(a, b): a ≤ b] is reflexive and transitive but is not symmetric.

(v) Let A = {1, 2, 3, 4} and relation R is defined on set A, such that for any a and b
R = {(a, b) : 0 < |a - b| ≤ 3}
or R = {(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4, 3)}

(a) R is symmetric, since .
(1, 2) ∈ R ⇒ (2, 1) ∈ R
Similarly, (1, 3) ∈ R ⇒ (3, 1) ∈ R
(1, 4) ∈ R ⇒ (4, 1) ∈ R
(2, 3) ∈ R ⇒ (3, 2) ∈ R
and (3, 4) ∈ R ⇒ (4, 3) ∈ R, etc.

(b) R is transitive, since
(1, 2) ∈ R, (2, 3) ∈ R ⇒ (1, 3) ∈ R Similarly,
(1, 4) ∈ R, (4, 2) ∈ R ⇒ (1, 2) ∈ R
i.e., 1R4 and 4R2 ⇒ 1R2 etc.

(c) R is not reflexive, since (1, 1), (2, 2), (3, 3), (4, 4) do not exist in R.
Thus, relation R = {(a, b): 0 < |a - b| ≤ 3} is symmetric and transitive but not reflexive.

 

Question 11.
Show that the relation R in the set A of points in a plane given by R = {(P, Q): distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all points related to a point P ≠ (0,0) is the circle passing through P with origin as centre.
Answer:
Let point O, is origin in plane then relation R is defined in set A such that
R = {(P, Q): OP = OQ}
(i) Relation R is reflexive, since for any point P, its distance from origin O is x, then
OP = x
i.e., x = x
or xRx is true
or (x, x) ∈ R

(ii) R is symmetric, since if points P and Q are at x and y distance from origin, then
(P, Q) ∈ R ⇒ OP = OQ
⇒ x = y
⇒ y = x
⇒ OQ = OP
⇒ (Q, P) ∈ R
⇒ (y, x) ∈ R
(x, y) ∈ R ⇒ (y, x) ∈ R

(iii) R is transitive, since P, Q and S are three points in plane such that
(P, Q) ∈ R and (Q, S) ∈ R
⇒ OP = OQ and OQ = OS
⇒ OP = OS
⇒ (P, S) ∈ R
Thus (P, Q) ∈ R, (Q, S) ∈ R
⇒ (P, S) ∈ R
We see that according to the given condition, relation R is reflexive, symrnetric and transitive. Thus, given relation R is an equivalence; relation. Again, let P be any fixed point in plane and second point Q is in plane such that (P, Q) ∈ R, then
(P, Q) ∈ R ⇒ OP = OQ
⇒ Point Q moves in plane such that its distance from origin O(0, 0) is equal to the distance of point P from origin.
⇒ Locus of point Q is a circle whose centre is at origin.
[Fixed distance OP = radius of circle]
As shown in following figure:

Hence Proved.

 

Question 12.
Show that the relation R defined in the set A of all triangles as R = {(T₁, T₂) is similar to T₂} is equivalence relation. Consider three right angled triangles T₁ with sides 3, 4, 5; T₂ with sides 5, 12, 13 and T₃ with sides 6, 8,10. Which triangles among T₁, T₂ and T₃ are related ?
Answer:
According to the question,
A = Set of all triangles in plane
or A = {x : x, is a triangle in plane]
aqd relation R, on set A is defined such that
R = {(T₁ , T₂ ): T₁ , T₂ are similar}

(i) R is reflexive, since each triangle is similar to itself, i.e„
T₁ RT₁ is true
or (T₁ , T₁) ∈ R

(ii) R is symmetric, since if triangles T₁ and T₂ are similar then triangle T₂ will be similar to triangle T₁ i.e.,
T₁RT₂ ⇒ T₂RT₁
or (T₁, T₂) ∈ R ⇒ (T₂, T₁) ∈R

(iii) R is transitive, since if triangles T₁, T₂ are similar and T₂, T₃ are similar then T₁ and T₃ will be similar, i.e.,
T₁RT₂ and T₂RT₃ ⇒ T₁RT₃
or (T₁, T₂) ∈ R, (T₂, T₃) ∈ R ⇒ (T₁, T₃) ∈ R
We see that relation R on set A is reflexive, symmetric and transitive. Thus, R is equivalence relation on set A.
Again, 3, 4, 5 are sides of triangle T₁ 5, 12, 13 are sides of triangle T₂ and 6, 8, 10 are sides of triangle T₃. If we consider sides of triangles T₁ and T₃ then
36=48=510=1236=48=510=12
It means sides of triangles T₁ and T₃ are proportional. Hence, T₁ and T₃ are similar triangles, i.e., T₁RT₃ is true or (T₁, T₃) ∈ R.
Therefore, T₁ and T₃ are related to each other.
Hence Proved.

 

Question 13.
Show that the relation R defined in the set A of all polygons as R = {(P₁, P₂): P₁ and P₂ have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right angled triangle T with sides 3, 4 and 5 ?
Answer:
According to the question,
A = Set of all polygons in plane
or A = {x : x, is a polygon in plane}
and relation R on set A is defined as
R = {(P₁, P₂): P₁ and P₂ have same number of sides}

(i) Relation R is reflexive, since number of sides of a polygon is similar to number of sides of itself, i.e., If P₁ is any polygon then P₁RP₁ or (P₁, P₁) ∈ R is true.

(ii) Relation R is symmetric since, if polygon P₁ has n sides and polygon P₂ has n sides then polygon P₂ will have n sides and polygon P₁ will have n sides, i.e.,
P₁RP₂ ⇒ P₂RP₁
or (P₁, P₂) ∈ R ⇒ (P₂, P₁) ∈ R.

(iii) Relation R is transitive, since if polygon P₁ and P₂ have n sides and polygon P₂ and P₃ have n sides then polygon P₁ and P₃ will have n sides each, i.e.,
P₁RP₂, P₂RP₃ ⇒ P₁RP₃
or (P₁, P₂) ∈ R, (P₂, P₃) ∈ R ⇒ (P₁, P₃) ⇒ R
We see that relation R on set A is reflexive, symmetric and transitive. Thus, R is an equivalence relation on set A. Again, according to question, set A is set of all polygons lie in plane, i.e., set A consists of triangle, quadrilateral, pentagon, hexagon, heptagon etc. Since, we have to find set A related to right angle of sides 3,4 and 5, then by given relation, all the triangles having same sides (three sides) are related to right angled triangle of sides 3,4 and 5, i.e., if T is a triangle of sides 3, 4 and 5 then all the triangles of set A will be related to T.
Hence Proved.

Question 14.
Let L be the set of all lines in XY plane and R be the relation in L defined as R = {(L₁, L₂): L₁ is parallel to L₂}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.
Answer:
According to question,
Set L = Set of all lines in XY plane
or L = {x : x, is a line in XY-plane}
R is a' set defined on L such that
R = {(L₁, L₂): L₁ is parallel to L₂}
where L₁, L₂ ∈ L

(i) R is reflexive, since each line is parallel to itself, i.e.,
L₁ || L₁ is true.
or L₁RL₁ or (L₁, L₁) ∈ R

(ii) R is symmetric, since if line L₁ is parallel to line L₂ then line L₂ will be parallel to line L₁.
i.e., L₁ || L₂ ⇒ L₂ || L₁
or L₁RL₂ ⇒ L₂RL₁
or (L₁, L₂) ∈ R (L₂, L₁) ∈ R

(iii) R is transitive, since if line L₁ is parallel to line L₂ and line L₂ is parallel to line L₃ then line L₁ will be parallel to line L₃, i.e.,
L₁ || L₂, L₂ || L₃ ⇒ L₁ || L₃; L₁, L₂, L₃ ∈ L
or (L₁, L₂) ∈ R, (L₂, L₃) ∈ R ⇒ (L₁, L₃) ∈ R
or L₁RL₂, L₂RL₃ ⇒ L₁RL₃
We see that relation R is reflexive, symmetric and transitive on set L.
Again, slope of line y = 2x + 4 is 2.
Thus, set of all the lines related to line y = 2x + 4 will be those lines whose slope will be 2. In this way, set of lines related toy = 2x + 4 is y = 2x + k, where k is an arbitrary constant.

 

Question 15.
Let R be the relation in the set {1,2,3,4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}. Choose the correct answer:
(A) R is reflexive and symmetric but not transitive.
(B) R is reflexive and transitive but not symmetric,
(C) R is symmetric and transitive but not reflexive.
(D) R is an equivalence relation.
Answer:
Let A = {1, 2, 3, 4}, then relation R defined on A,
R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}
We see that for each a ∈ A, aRa is true.
i.e., (a, a) ∈ R, since
(1, 1), (2, 2), (3, 3), (4,4) ∈ R
Thus, R is reflexive.
Again, for a, b ∈ A
V (a, b) ∈ R ⇏ (b, a) ∈ R
Since (1, 2) ∈ R ⇏ (2, 1) ∈ R
(1, 3) ∈ R ⇏ (3, 1) ∈ R
i.e., 1R2 ⇏ 2R1
1R3 ⇏ 3R1
Thus, R is not symmetric.
For a, b, c ∈ A
(a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∈ R
Since, (1, 1) ∈ R, (1, 2) ∈ R ⇒ (1, 2) s R, is true.
(1, 3) ∈ R, (3, 3) ∈ R ⇒ (1, 3) ∈ R, is true.
(1, 3) ∈ R, (3, 2) ∈ R ⇒ (1, 2) ∈ R, is true.
Thus, R is transitive.
We see that relation R on set A is reflexive, transitive but not symmetric.
Thus, (B) is correct.

Question 16.
Let R be the relation in the set N given by R = [(a, b): a = b - 2, b > 6}. Choose the correct answer:
(A) (2, 4) ∈R
(B) (3, 8) ∈ R
(C) (6, 8) ∈ R
(D) (8, 7) ∈ R
Answer:
According to the question
N = Set of natural numbers
or N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, .......... }
And relation R on set N is defined in the following way:
R = {(a, b): a = b - 2, b > 6}, where a, b ∈ N
a = b - 2, b > 6
Putting, b = 8, we have a = 8 - 2 = 6
Then (6, 8) ∈ R, which is given in (C).
Thus, option (C) is correct answer.

सभी प्रकार के नोट्स TOPPRS.IN पर FREE उपलब्ध है !